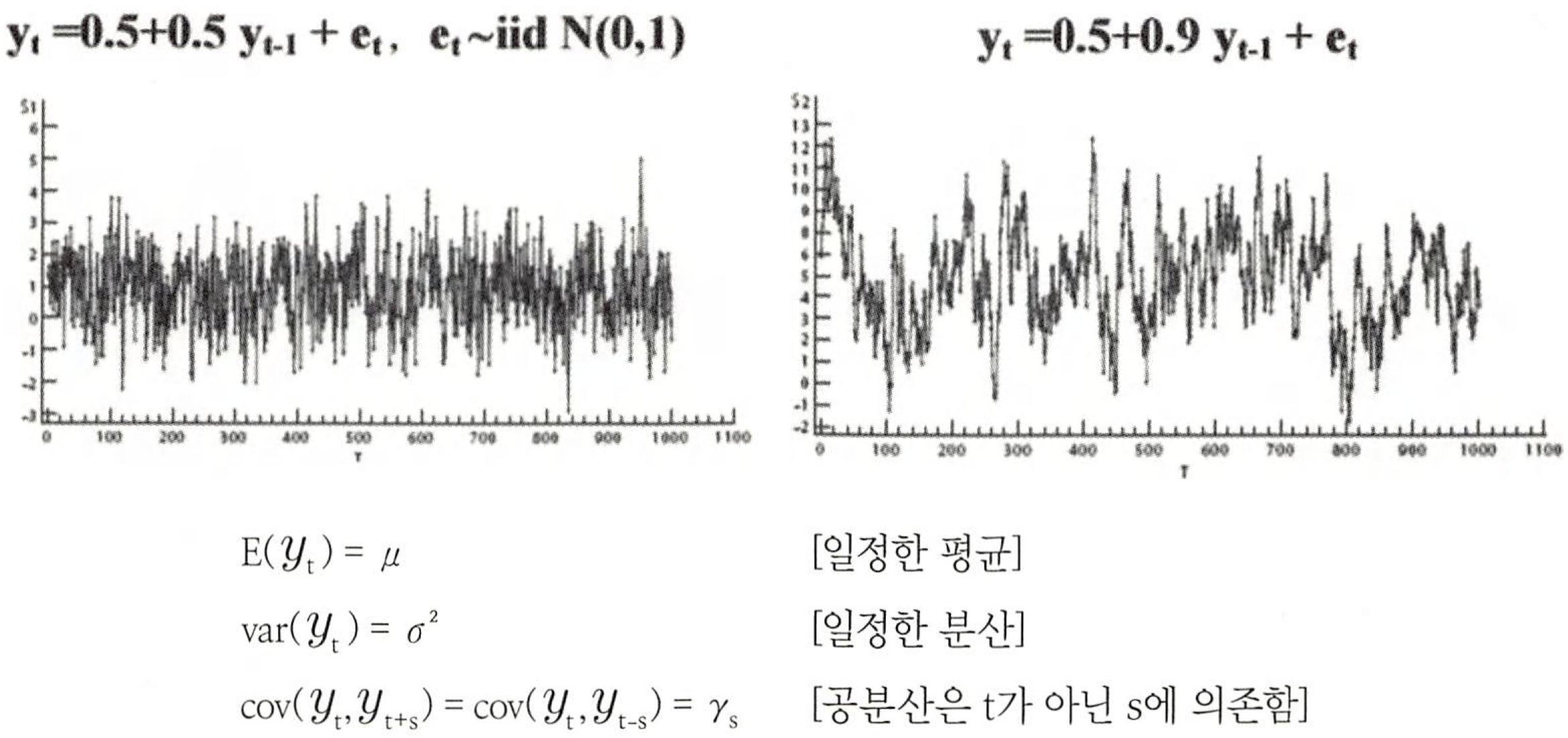
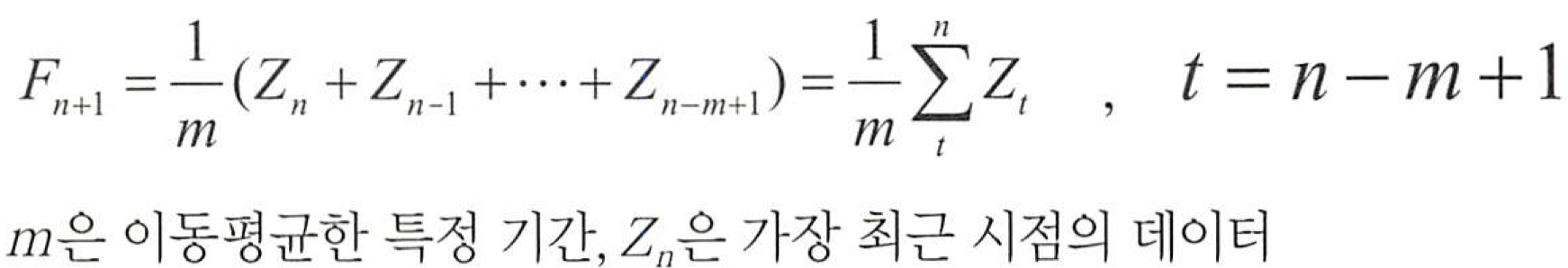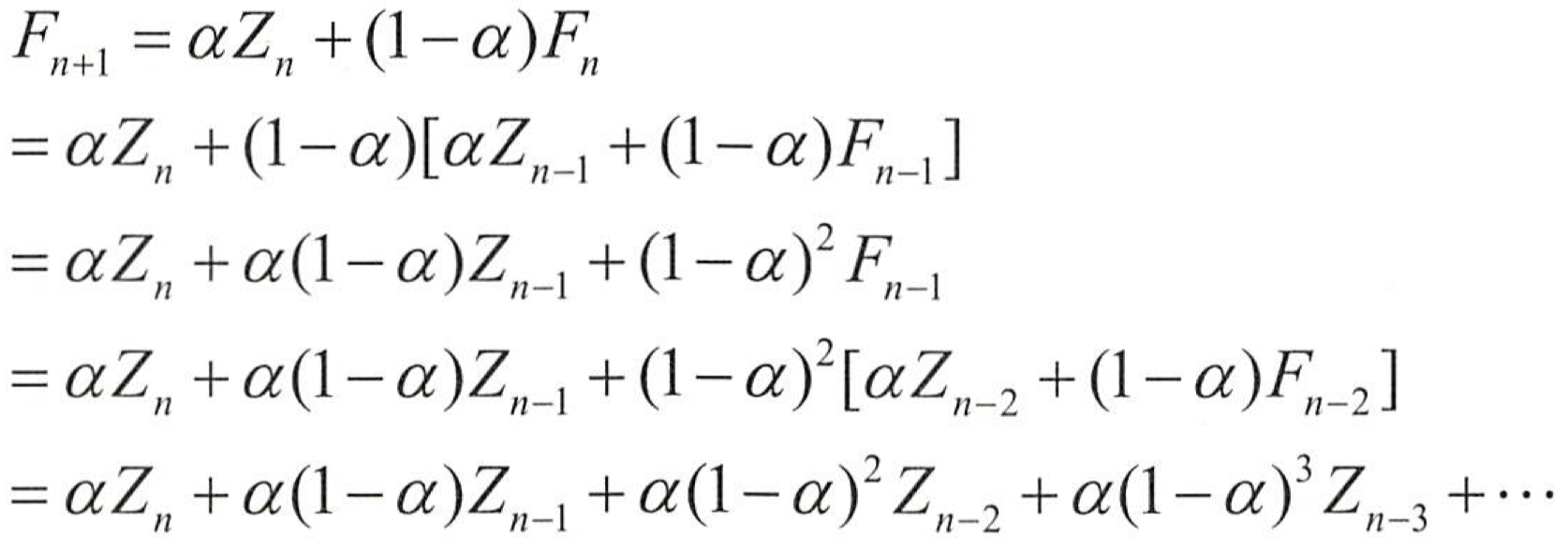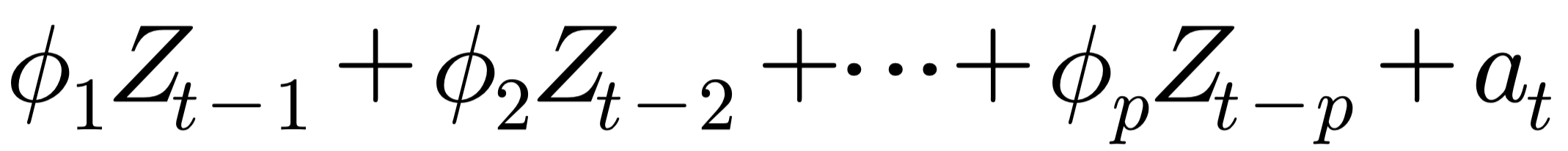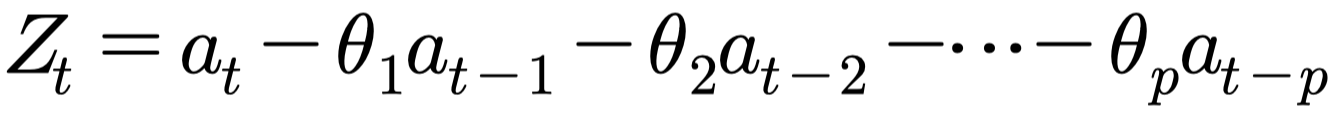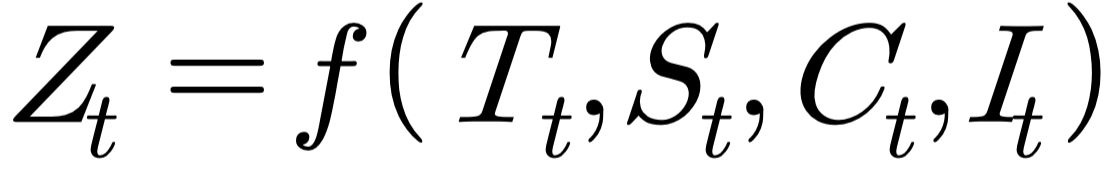Post

[R] 시계열 분석

Posted
By LEE KWANGHO
24 min read
[R] 시계열 분석

#01. 시계열 분석 개요

1) 시계열 자료

시계열 자료 개요

  • 시간의 흐름에 따라 관찰된 값들
  • 시계열 데이터의 분석을통해 미래의 값을 예측하고 경향, 주기, 계절성 등을 파악하여 활용한다.

시계열 자료의 종류

  1. 비정상성 시계열 자료 - 시계열 분석을 실시할 때 다루기 어려운 자료로 대부분의 시계열자료.
  2. 정상성 시계열 자료- 비정상 시계열을 핸들링해 다루기 쉬운 시계열 자료로 변환한 자료

2) 정상성 🌟

평균이 일정할 경우

  • 모든 시점에 대해 일정한 평균을 가진다 .
  • 평균이 일정하지 않은 시계열은 차분 (difference )을 통해 정상화할 수 있다 .

분산이 일정

  • 분산도 시점에 의존하지 않고 일정해야 한다 .
  • 분산이 일정하지 않을 경우 변환(Transformation )을 통해 정상화할 수 있다.

공분산도 단지 시차에만 의존, 실제 특정 시점 t, s 에는 의존하지 않는다.

약한의미의 정상성

  • 모든 시점에 평균일정, 시점과 분산 독립, 공분산은 시차에만 의존

비정상→정상 : 변환(transformation), 차분(difference)

  • 변환 : 분산이 일정하지 않은 비정상 시계열
  • 차분(t1-t0) : 평균이 일정하지 않은 비정상 시계열
  • 일반차분 (regular difference) : 바로 전 시점의 자료를 빼는 방법이다 .
  • 계절차분 (seasonal difference) ：여러 시점 전의 자료를 빼는 것 방법 , 주로 계절성을 갖는 자료를 정상화 하는데 사용한다 .

#02. 정상시계열

  • 정상 시계열은 어떤 시점에서 평균과 분산 그리고 특정한 시차의 길이를 갖는 자기공분산을 측정하더라도 동일한 값을 갖는다.
  • 정상 시계열은 항상 그 평균값으로 회귀하려는 경향이 있으며，그 평균값 주변에서의 변동은 대체로 일정한 폭을 갖는다.
  • 정상 시계열이 아닌 경우 특정 기간의 시계열 자료로부터 얻은 정보를 다른 시기로 일반화 할 수 없다.

/images/2022/1228/img_0.png

#03. 시계열 분석 모형

1) 분석방법 종류

분석방법에 따른 구분

이름태그설명
수학적 이론 모형Box-Jenkins, 회귀분석(계량경제) 
직관적 방법시계열 분해법, 지수평활법시간에 따른 변동이 느린 데이터 분석에 활용
장기 예측회귀분석방법 
단기 예측Box-Jenkins, 시계열 분해법, 지수평활법 

자료 형태에 따른 구분

이름태그설명
일변량 시계열분석Box-Jenkins(ARMA), 시계열 분해법, 지수 평활법시간 (t)을 설명변수로 한 회귀모형주가，소매물가지수 등 하나의 변수에 관심을 갖는 경우의 시계열분석
다중 시계열분석다변량 ARIMA, 개입분석, 계량경제 모형, 상태공간 분석, 전이함수 모형여러개의 시간(t)에 따른 변수들을 활용하는 시계열 분석

3) 이동평균모형(MA모형) 🧨

이동평균법의 개념

  • 과거로부터 현재까지의 시계열 자료를 대상으로 일정기간별 이동평균을 계산하고，이들의 추세를 파악하여 다음 기간을 예측하는 방법
  • 시계열 자료에서 계절변동과 불규칙변동을 제거하여 추세변동과 순환변동만 가진 시계열로 변환하는 방법으로도 사용됨

/images/2022/1228/img_1.png

  • n 개의 시계열 데이터를 m 기간으로 이동평균하면 n-m+1 개의 이동평균 데이터가 생성된다.

이동평균법의 특징

  • 간단하고 쉽게 미래를 예측
  • 자료의 수가 많고 안정된 패턴을 보이는 경우 예측의 품질이 높음
  • 특정 기간 안에 속하는 시계열에 대해서는 동일한 가중치를 부여함
  • 일반적으로 시계열 자료에 뚜렷한 추세가 있거나 불규칙변동이 심하지 않은 경우에는 짧은 기간 (m의 개수를 적음)의 평균을 사용, 반대로 불규칙변동이 심한 경우 긴 기간 (m의 개수가 많음) 의 평균을사용함
  • 이동평균법에서 가장 중요한 것은 적절한 기간을 사용하는 것. 즉, 적절한 n 의 개수를 결정 하는 것임.

4) 지수평활법 🧨

지수평활법의 개념

  • 일정기간의 평균을 이용하는 이동평균법과 달리 모든 시계열 자료를 사용하여 평균을 구하며, 시간의 흐름에 따라 최근 시계열에 더 많은 가중치를 부여하여 미래를 예측하는 방법.

/images/2022/1228/img_2.png

  • 여기서 Fn+1은 n 시점 다음의 예측값，a 는 지수평활계수，Z n은 n 시점의 관측값.
  • 지수평활 계수가 과거로 갈수록 지수형태로 감소하는 형태

지수평활법의 특징

  • 단기간에 발생하는 불규칙변동을 평활하는 방법
  • 자료의 수가 많고，안정된 패턴을 보이는 경우일수록 예측 품질이 높음
  • 지수평활법에서 가중치의 역할을 하는 것은 지수평활계수 (a) 이며 , 불규칙변동이 큰 시계열의 경우 지수평활계수는 작은 값을，불규칙변동이 작은 시계열의 경우 , 큰 값의 지수평활계수를 적용함
  • 지수평활계수는 예측오차(실제 관측치와 예측치 사이의 잔차제곱합)를 비교하여 예측오차가 가장 작은 값을 선택하는 것이 바람직함
  • 지수평활계수는 과거로 갈수록 지속적으로 감소함
  • 지수평활법은 불규칙변동의 영향을 제거하는 효과가 있으며，중기 예측 이상에 주로 사용됨 (단，단순지수 평활법의 경우，장기추세나 계절변동이 포함된 시계열의 예측에는 적합하지 않음)

#04. 시계열 모형 🌟

1) 자기회귀모형(AR모형)

  • p시점 전의 자료가 현재 자료에 영향을 주는 자귀회귀모형을 AR(p) 모형이라 함

/images/2022/1228/img_3.png

  • $a_t$ : white noise process(백색잡음과정)
  • 자귀회귀모형 판단 조건 : 자기상관함수(ACF) 빠르게 감소하고 부분자기상관함수(PACF)는 어느 시점에 절단점 갖음

2) 이동평균모형(MA모형)

  • 유한한 개수의 백색잡음의 결합. 항상 정상성 만족

/images/2022/1228/img_4.png

  • ACF에서 절단점 갖고 PACF가 빠르게 감소

3) 자기회귀누적이동평균모형(ARIMA(p,d,q)모형) 🌟🌟🌟

  • 가장 일반적인 모형
  • 비정상시계열 모형
  • 차분이나 변환을 통해 AR/MA/ARMA 모형으로 정상화 가능
  • p는 AR, q는 MA와 관련있는 차수로 ARIMA에서 ARMA로 정상화할 때 차분한 횟수 의미
  • d=0 이면 ARMA(p,q) 모형이라 부르고，이모형은 정상성을 만족한다 .(ARM A(0,0) 일 경우 정상 화가 불필요하다)
  • p=0 이면 IMA(d, q) 모형이라고 부르고 , d번 차분하면 MA(q) 모형을 따른다 .
  • q=0 이면 ARI(p, d) 모형이라 부르며, d 번 차분한 시계열이 AR(p) 모형을 따른다 .

예시

  • ARIMA(0, 1, 1)의 경우에는 1차분 후 MA(1) 활용
  • ARIMA(1, 1, 0)의 경우에는 1차 분 후 AR(1) 활용

4) 분해 시계열

  • 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
  • 회귀분석적 방법 주로 사용
  • 시계열 구성 요소 🌟
    1. 추세요인(trend factor) : 자료가 어떤 특정한 형태를 취할 때
    2. 계절요인(seasonal factor) : 고정된 주기에 따라 자료가 변화
    3. 순환요인(cyclical factor) : 알려지지 않은 주기를 갖고 자료가 변화
    4. 불규칙요인(irregular factor) : 회귀분석에서 오차에 해당하는 요인
  • 분해시계열분석법에서는 각 구성요인을 정확히 분리하는 것이 중요
  • 요인 정확히 분리하기 쉽지 않으며 이론적 약점 존재 but 많이 사용됨

/images/2022/1228/img_5.png

#05. 시계열 분석 R 실습 (1)

1) 필요한 패키지 및 데이터 가져오기

패키지 로드

1
2
3
4
5
6
7
8
9

REPO_URL <- "https://cran.seoul.go.kr/"

if (!require("tseries")) install.packages("tseries", repos=REPO_URL)
if (!require("forecast")) install.packages("forecast", repos=REPO_URL)
if (!require("TTR")) install.packages("TTR", repos=REPO_URL)

library(tseries)
library(forecast)
library(TTR)

데이터 가져오기

1
2

kings <- read.csv("http://itpaper.co.kr/demo/r/kings.csv", stringsAsFactors=F, fileEncoding="utf-8")
head(kings)

💻 출력결과

/images/2022/1228/img_6.png

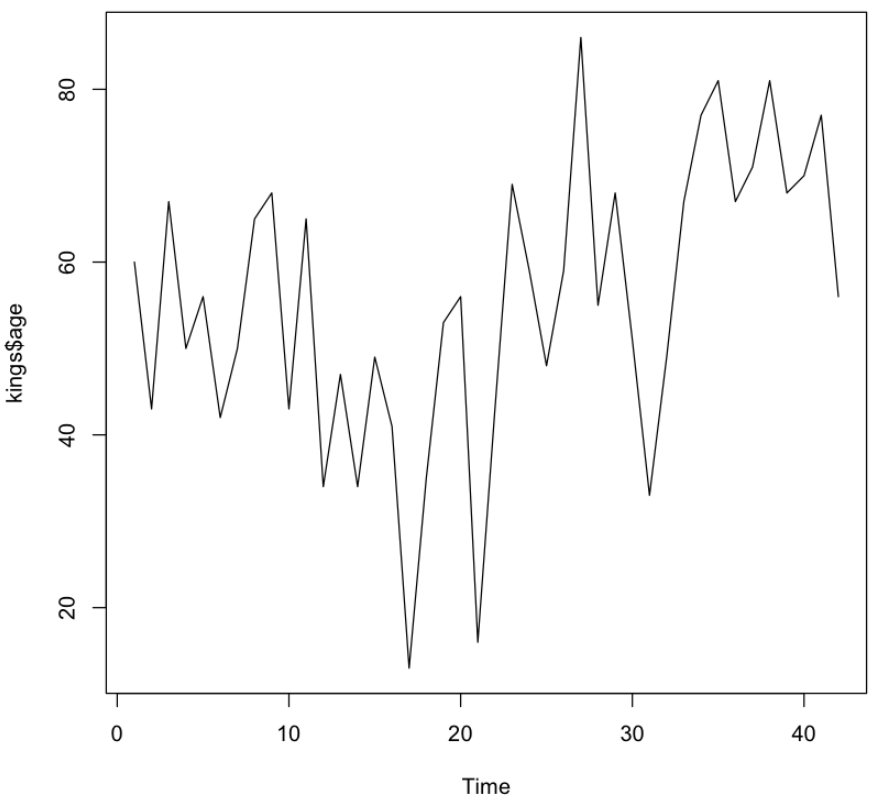
2) 시계열 그래프 그리기

plot.ts() 함수를 사용하여 시계열 데이터를 선 그래프 형태로 표현한다.

숫자로만 구성된 변수를 파라미터로 전달하게 되는데 이 데이터들은 y축에 해당하고 x축은 시간의 흐름(time)으로 자동 설정된다.

기본 형태의 시계열 그래프

1

plot.ts(kings$age)

💻 출력결과

/images/2022/1228/img_7.png

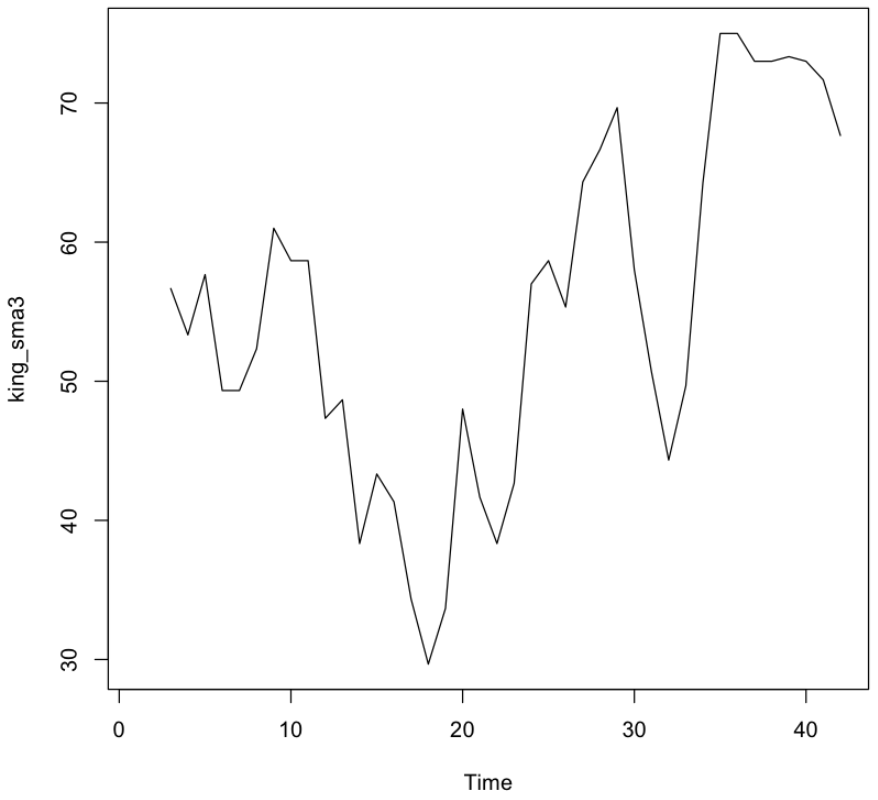
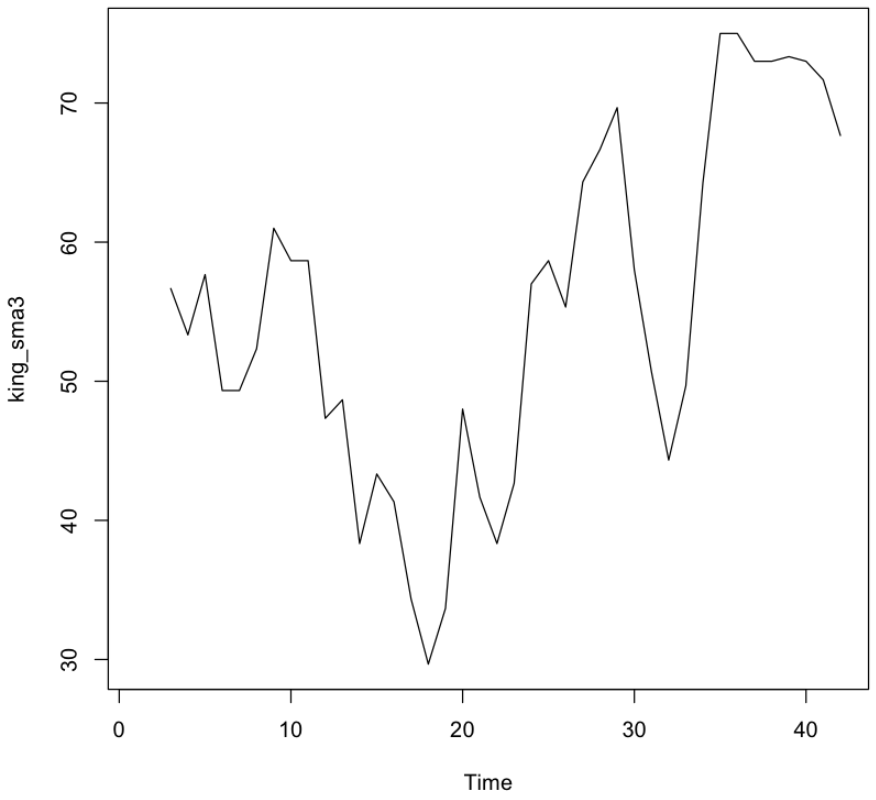
3년마다 평균을 내서 그래프를 부드럽게 표현

1
2

king_sma3 <- SMA(kings$age, n=3)
plot.ts(king_sma3)

💻 출력결과

/images/2022/1228/img_8.png

8년마다 평균을 내서 그래프를 부드럽게 표현

1
2

king_sma8 <- SMA(kings$age, n=8)
plot.ts(king_sma3)

💻 출력결과

/images/2022/1228/img_9.png

이동 평균 한번에 보기

1
2
3
4
5
6
7
8
9
10

kings_sma3 <- SMA(kings$age, n = 3)
kings_sma8 <- SMA(kings$age, n = 8)
kings_sma12 <- SMA(kings$age, n = 12)

par(mfrow = c(2,2))

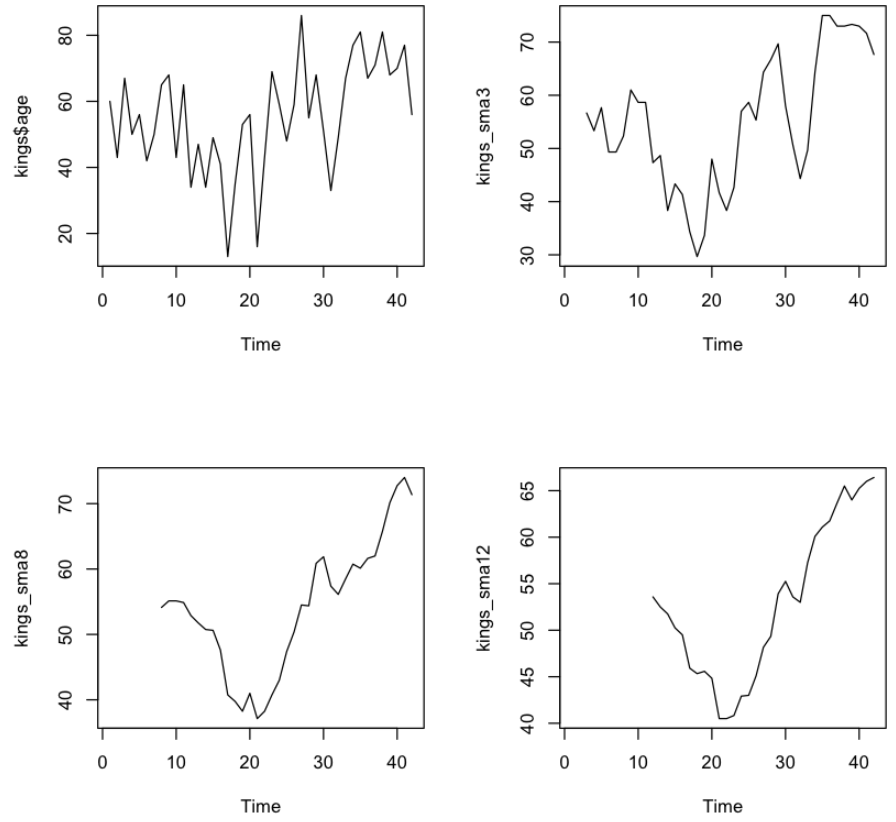
plot.ts(kings$age)
plot.ts(kings_sma3)
plot.ts(kings_sma8)
plot.ts(kings_sma12)

💻 출력결과

/images/2022/1228/img_10.png

3) ARIMA 모델 적용

데이터 정상화

ARIMA 모델은 정상성 시계열에 한해 사용한다 .

  • 비정상 시계열 자료는 차분해 정상성으로 만족하는 조건의 시계열로 바꿔준다 .
  • 이전 그래프에서 평균이 시간에 따라 일정치 않은 모습을 보이므로 비정상시계열이다 .

따라서 차분을 진행한다 .

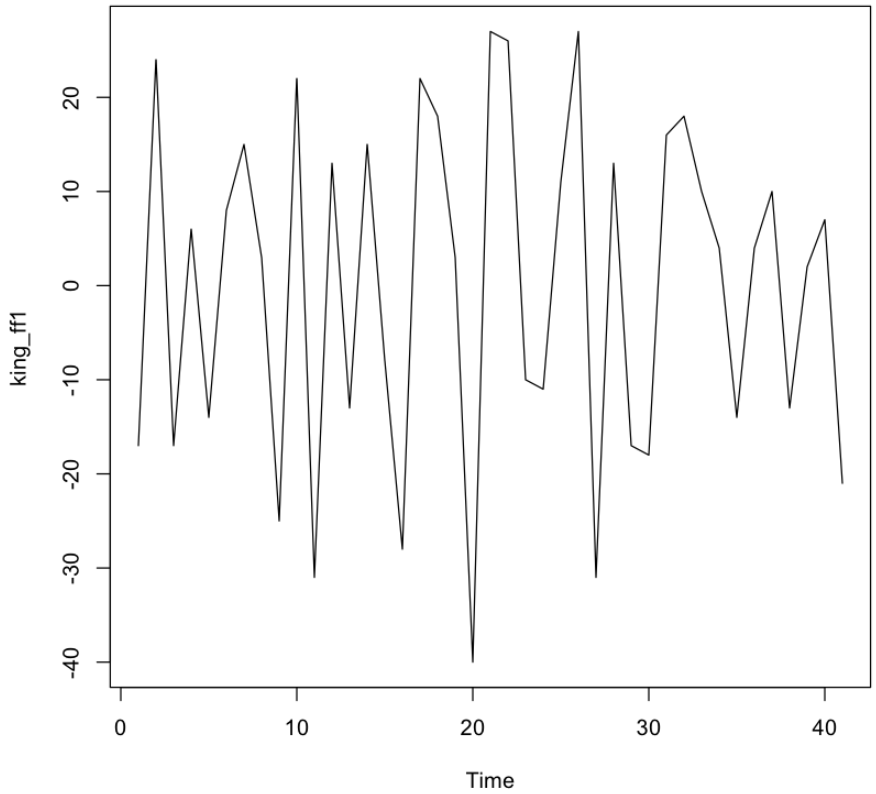
  • 1차 차분 결과에서 평균과 분산이 시간에 따라 의존하지 않음을 확인한다 .
  • ARIMA(p, 1, q)모델이며 차분을 1번 해야 정상성을 만족한다.
  • 1차 차분 진행
1
2

king_ff1 <- diff(kings$age, differences=1)
plot.ts(king_ff1)

💻 출력결과

/images/2022/1228/img_11.png

ACF와 PACF 를 통한 적합한 ARIMA 모델 결정

ACF

1
2

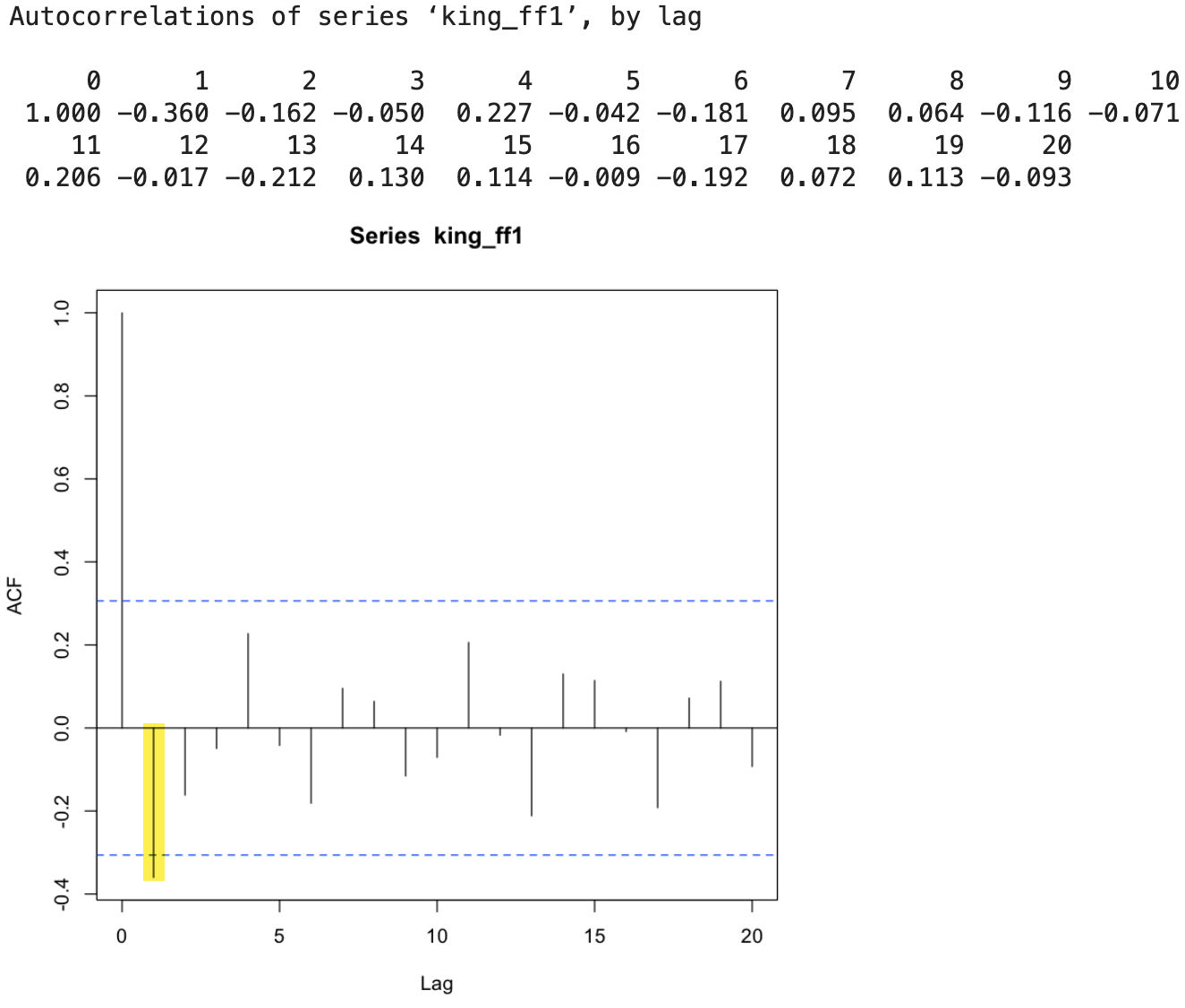
acf(king_ff1, lag.max=20)
acf(king_ff1, lag.max=20, plot=FALSE)

💻 출력결과

/images/2022/1228/img_12.png

💡 lag 는 0부터 값을 갖는데，너무 많은 구간을 설정하면 그래프를 보고 판단하기 어렵다. * ACF값이 lag 1인 지점 빼고는 모두 점선 구간 안에 있고 , 나머지는 구간 안에 있다.

PCAF

1
2

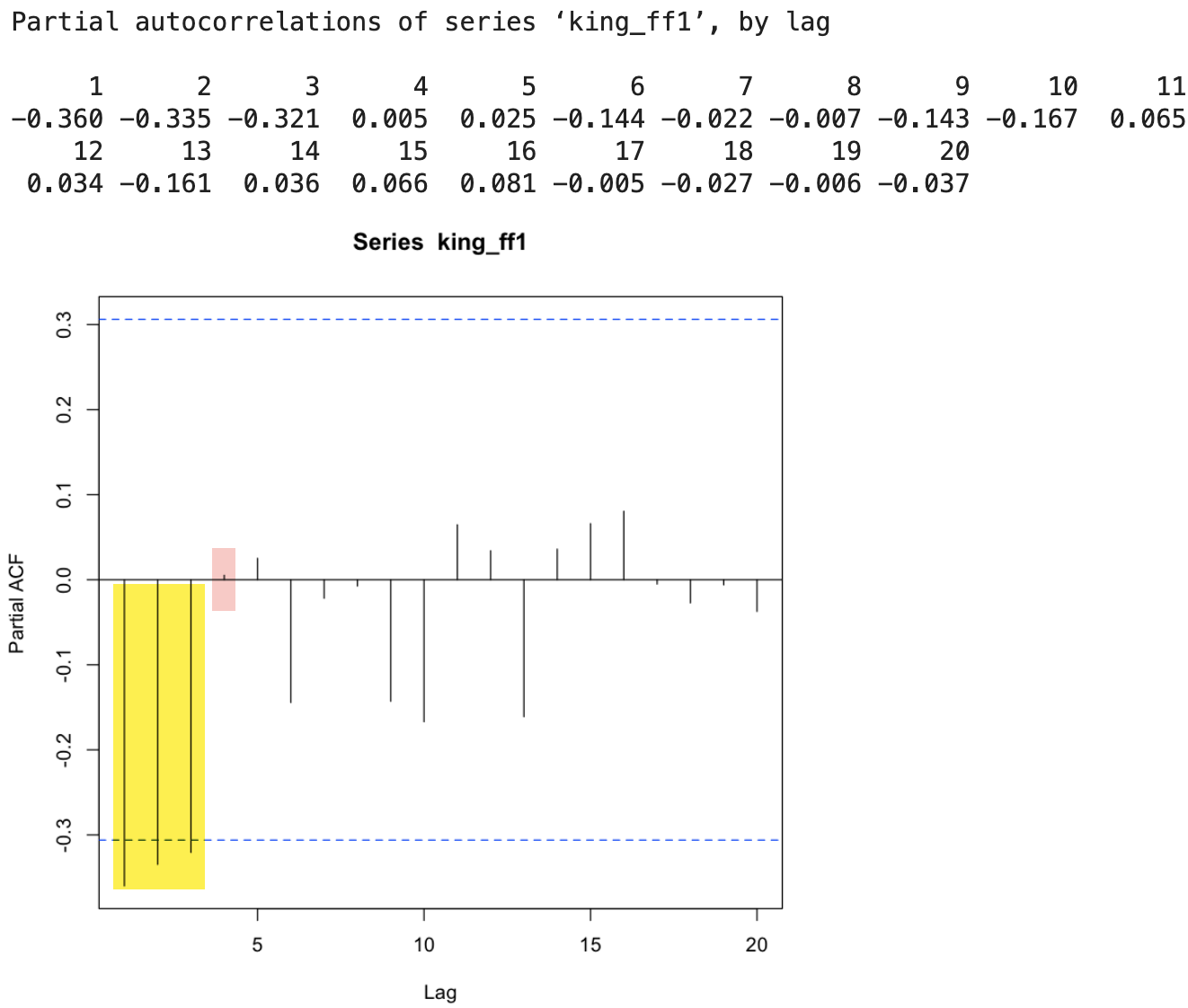
pacf(king_ff1, lag.max=20)
pacf(king_ff1, lag.max=20, plot=FALSE)

💻 출력결과

/images/2022/1228/img_13.png

💡 PACF - PACF 값이 lag 1, 2, 3에서 점선 구간을 초과하고 음의 값을 가지며 절단점이 lag 4 이다 .

4) 종합

  • ARMA 후보들이 생성
  • ARMA(3, 0) 모델 : PACF 값이 lag4 에서 절단점을 가짐. → ARMA(3)모형
  • ARMA(0, 1) 모델 : ACF 값이 lag2 에서 절단점을 가짐 → MA(1)모형
  • ARMA(p，q) 모델 : 그래서 AR모형과 MA모형을 혼합

5) 적절한 ARIMA 모형 찾기

  • forecast package 에 내장된 auto.arima() 함수 이용
  • ARMIA 모형 찾기
1

auto.arima(kings$age)

💻 출력결과

1
2
3
4
5
6
7
8
9
10

Series: kings$age
ARIMA(0,1,1)

Coefficients:
          ma1
      -0.7218
s.e.   0.1208

sigma^2 estimated as 236.2:  log likelihood=-170.06
AIC=344.13   AICc=344.44   BIC=347.56

💡 영국 왕의 사망 나이 데이터의 적절한 ARIMA모형은 ARIMA(0, 1, 1)이다 .

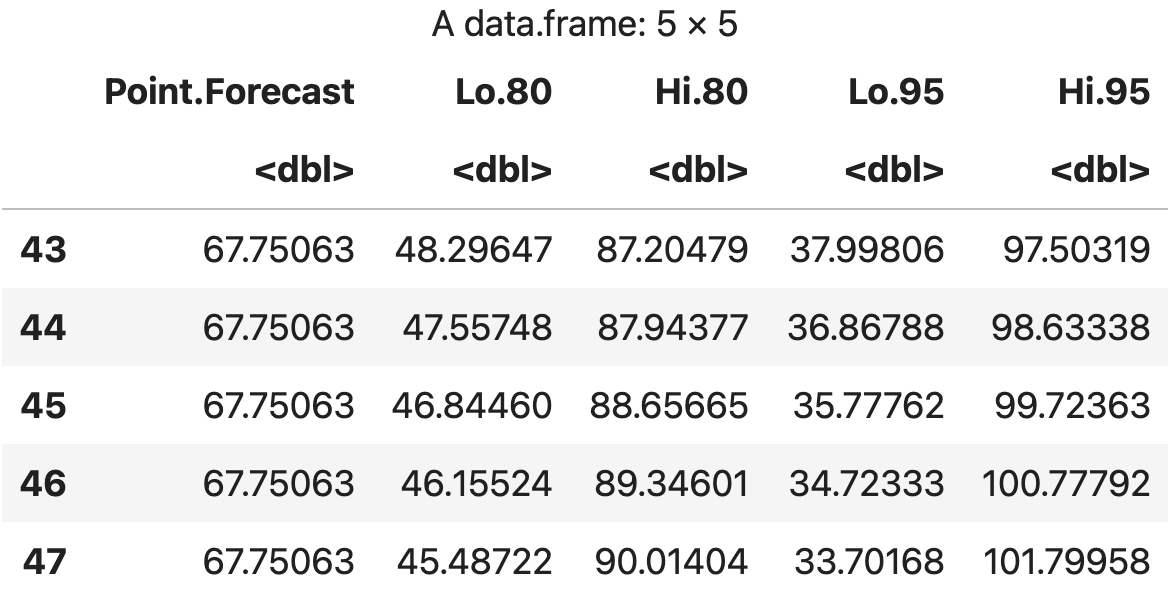
6) 예측

arima 결과를 활용한 forecast 예측

  • 42 명의 영국왕 중에서 마지막 왕의 사망시 나이는 56 세
  • 43 번째에서 52번째 왕까지 10명의 왕의 사망시 나이를 예측한 결과 67.75살로 추정된다 .
  • 5 명 정도만 예측하고 싶다면，옵션에 h=5 를 입력한다 .
  • 신뢰 구간은 80%~95% 사이
  • 시계열 분석을 통한 영국 왕들의 사망시 나이 예측
1
2
3
4

king_arima <- arima(kings$age, order=c(0, 1, 1))
king_forecasts <- forecast(king_arima)
df <- data.frame(king_forecasts)
df

💻 출력결과

/images/2022/1228/img_14.png

예측결과 시각화

1

plot(king_forecasts)

💻 출력결과

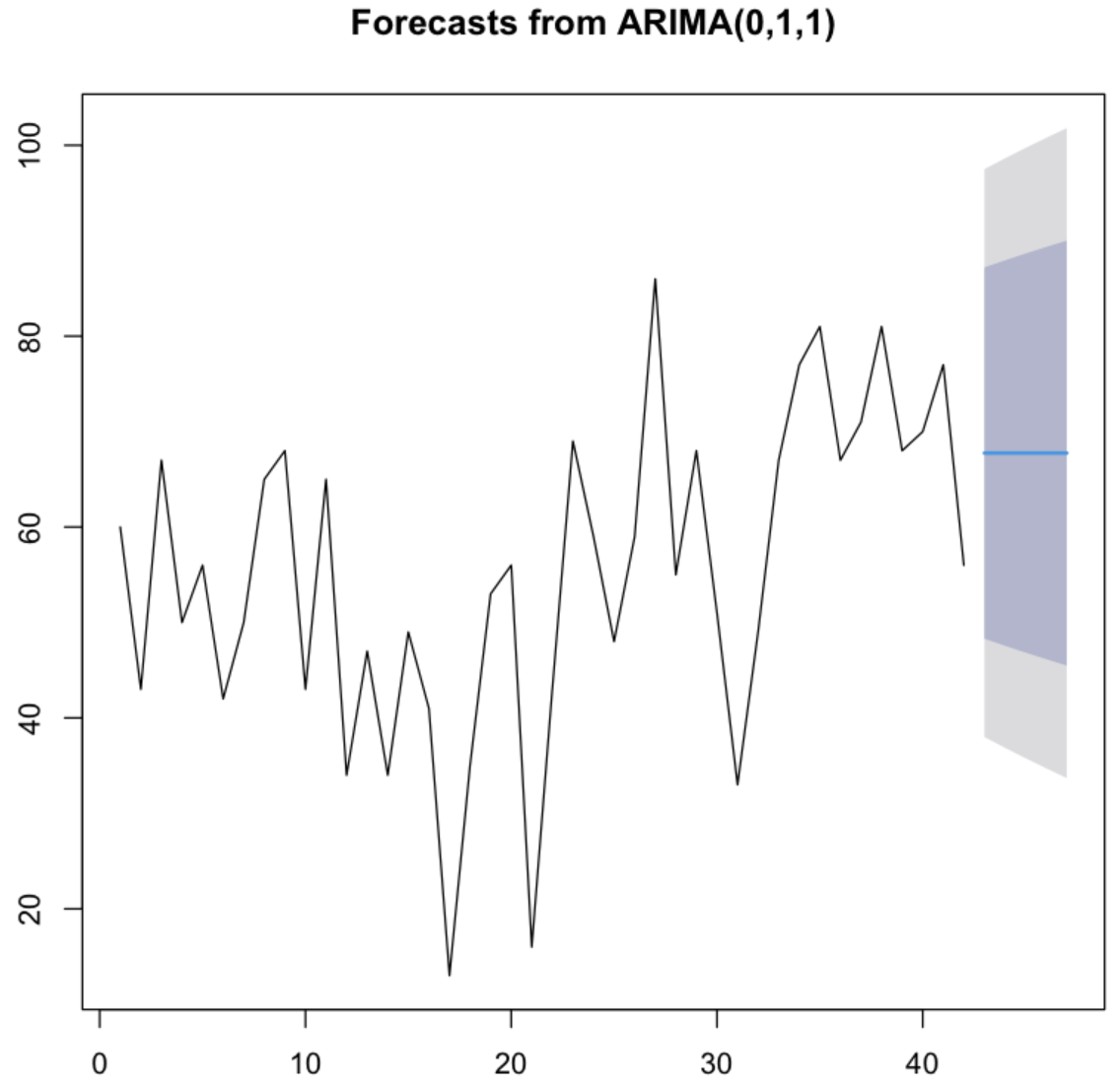
/images/2022/1228/img_15.png

💡 진한 파란선이 점추정과 같은 회귀선이고 가장 높은 옅은 파란 영역(80%)과 회색영역(95%)이 신뢰구간인 구간예측값이다.

#06. 시계열 분석 R 실습 (2)

Nile 은 나일강 연간 유입량에 관한 데이터로서 R에 기본 내장되어 있다.

1) 데이터 가져오기

  • 데이터 가져오기
1
2

df <- data.frame(Nile)
head(df)

💻 출력결과

/images/2022/1228/img_16.png

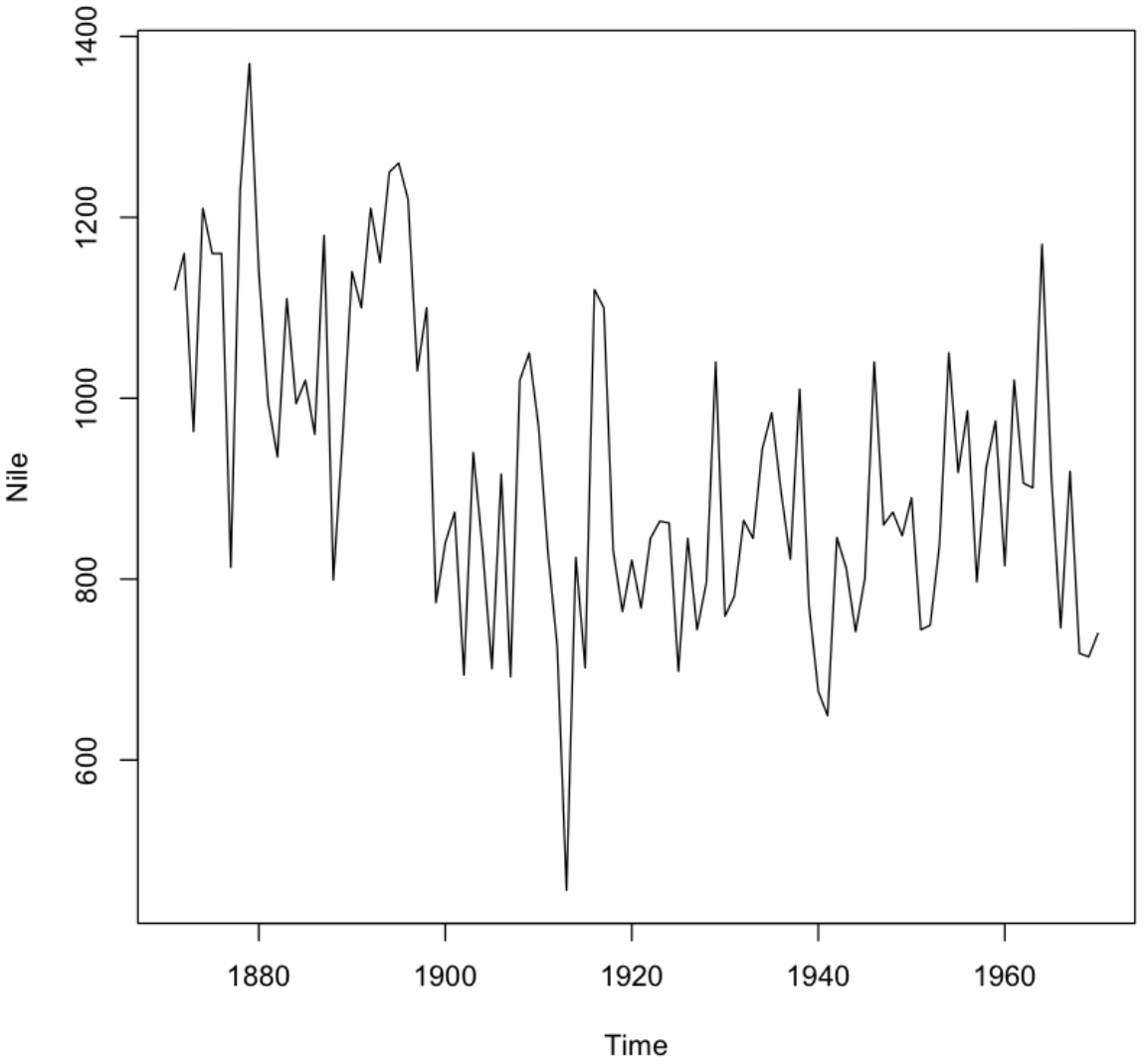
2) 시계열 그래프 그리기

나일강 데이터를 먼저 살펴보면 규칙적인 계절성이 띄는 것 같아 보이지 않는다.

하지만, 평균이 변화하는 추세는 약간 보이는 듯 하다. 그렇기에 정상성을 만족하지 못한다.

기본 형태의 시계열 그래프

  • 기본 형태의 시계열 그래프 그리기
1

plot.ts(Nile)

💻 출력결과

/images/2022/1228/img_17.png

3) ARIMA 모델 적용

데이터 정상화

R에서 차분은 diff함수를 통해서 정할 수 있다. diff(ts, differences = d-횟수)를 사용하면, 원하는 d만큼 차분이 가능하다.

  • 1차 차분 진행
1
2

Nile.diff_1 <- diff(Nile, differences = 1)
plot(Nile.diff_1)

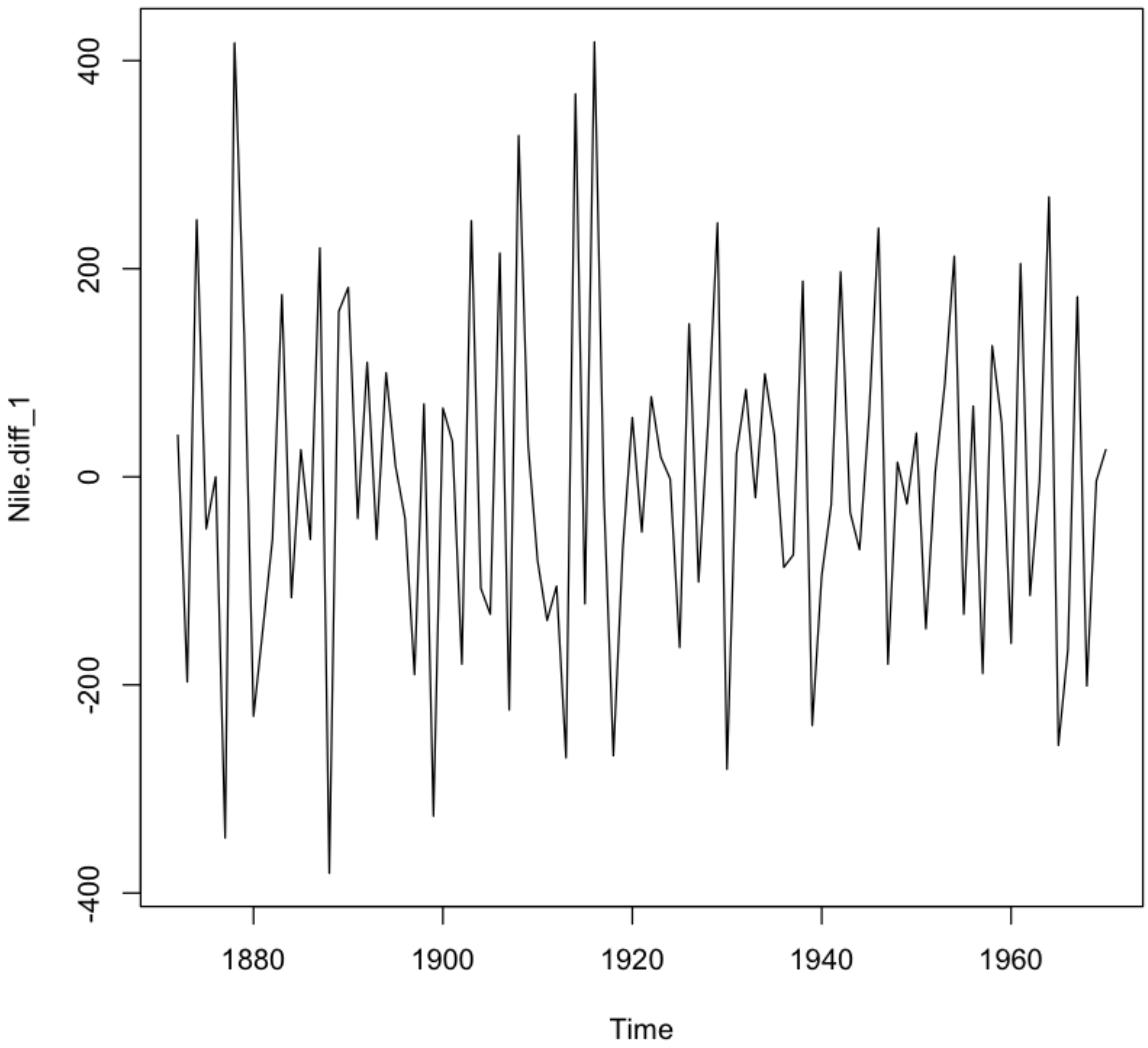
💻 출력결과

/images/2022/1228/img_18.png

1번 차분을 한 결과 원 데이터보다는 평균이 일정해진 것처럼 보인다. 하지만 명확하지 않다. 한번 더 해보자.

  • 2차 차분 진행
1
2

Nile.diff_2 <- diff(Nile, differences = 2)
plot(Nile.diff_2)

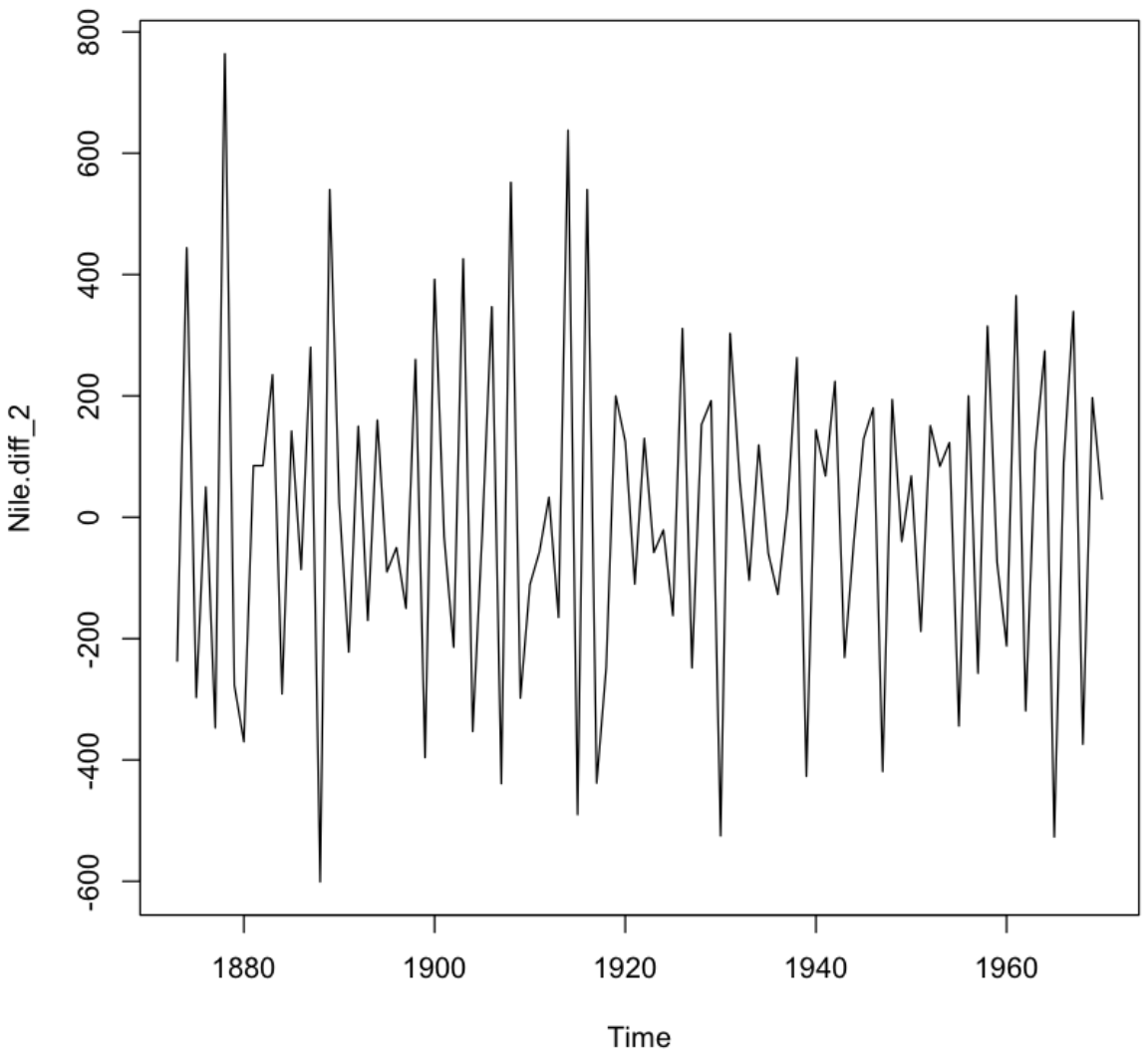
💻 출력결과

/images/2022/1228/img_19.png

💡 차분을 2회 진행하니 1회 진행한 것보다도 평균과 분산이 시간이 지남에 따라서 일정한 정상성을 띄는 것을 확인할 수 있다. 이제 이 차분을 진행한 데이터 Nile.diff_2를 사용하여 자기상관함수와 부분자기상관함수를 통해서 AR/MA 모형의 여부를 살펴보자.

ACF와 PACF 를 통한 적합한 ARIMA 모델 결정

ACF 자기상관함수 그래프

1

acf(Nile.diff_2, lag.max=20)

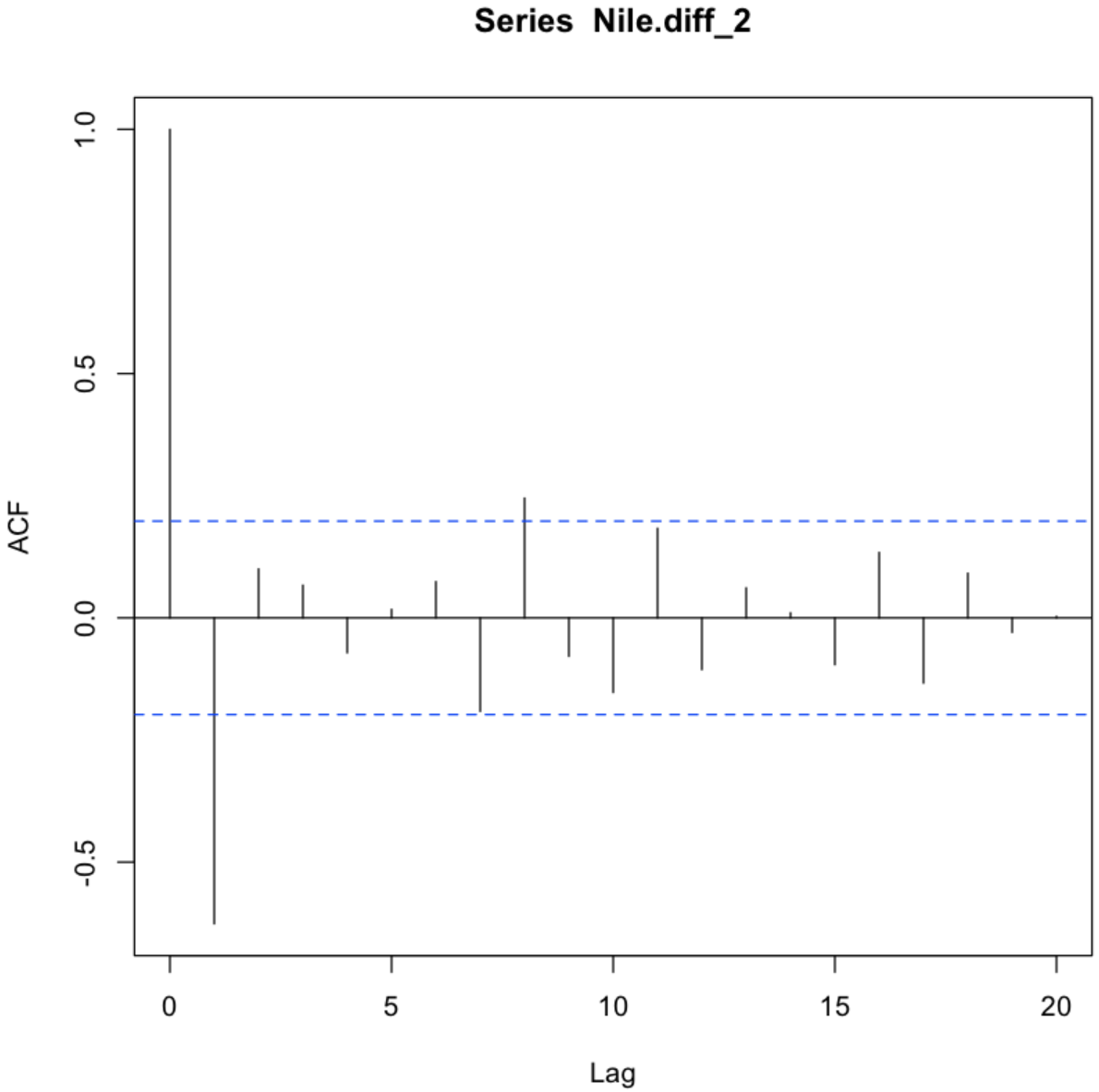
💻 출력결과

/images/2022/1228/img_20.png

💡 1번째와 8번째 lag를 제외하고는 모두 신뢰구간안에 포함되어 있다.

ACF 자기상관함수 도표

1

acf(Nile.diff_2, lag.max=20, plot = FALSE)

💻 출력결과

/images/2022/1228/img_21.png

PCAF 부분 자기 상관함수 그래프

1

pacf(king_ff1, lag.max=20)

💻 출력결과

/images/2022/1228/img_22.png

PCAF 부분 자기 상관함수 도표

1

pacf(king_ff1, lag.max=20, plot = FALSE)

💻 출력결과

/images/2022/1228/img_23.png

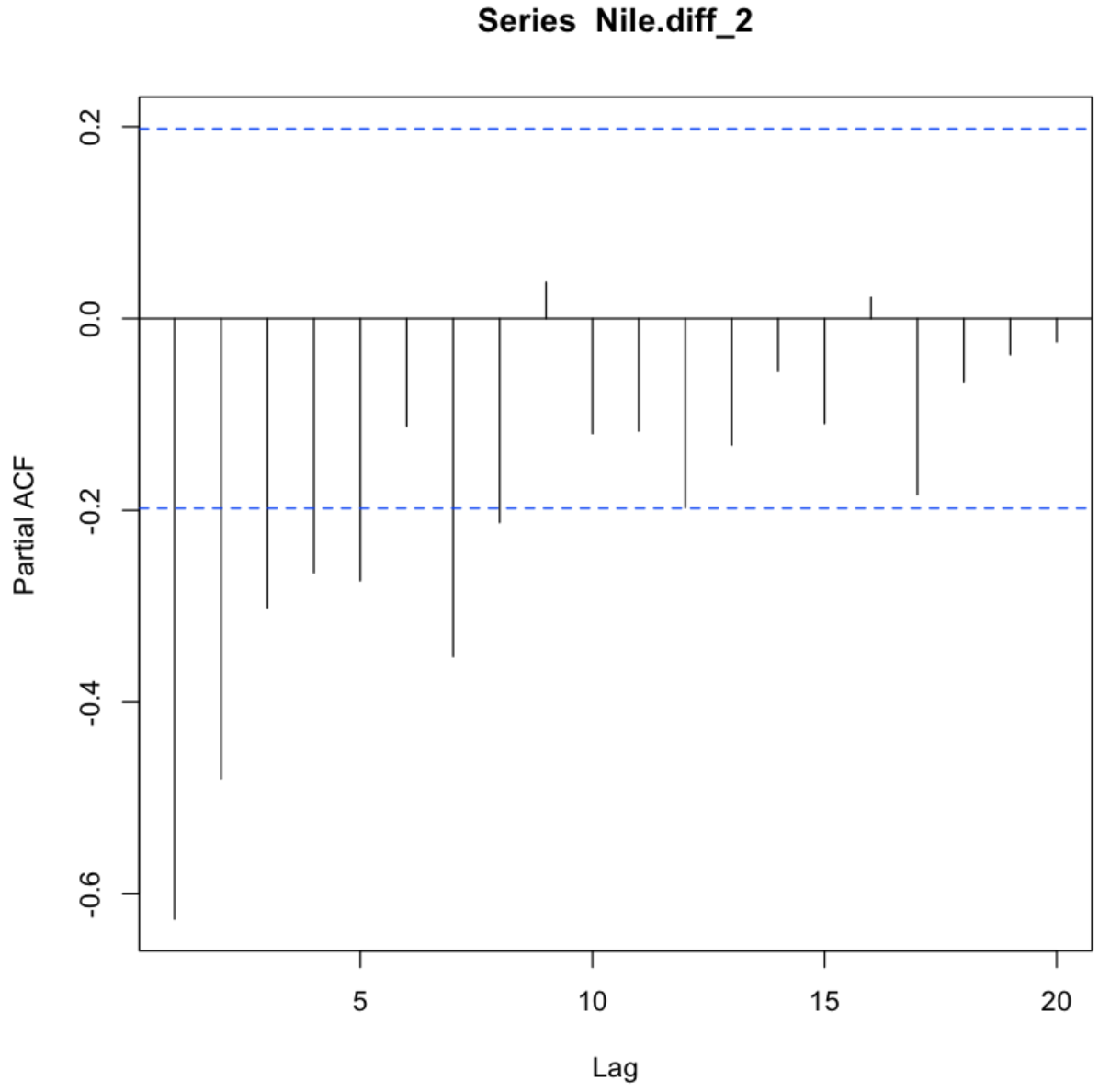
4) 종합

부분자기상관함수는 pacf함수를 통해서 확인할 수 있다. 사용방법은 acf와 동일하다. 부분자기상관함수는 lag 1~8신뢰구간을 넘어 음의 값을 가지고 lag 9에서 절단이 된 것을 확인할 수 있다.

자기상관함수(ACF)와 부분자기상관함수(PACF)를 확인해 본 결과,

  • $ARMA(8,0)$ 부분자기상관함수 그래프를 볼 때, lag 9에서 절단
  • $ARMA(0,1)$ 자기상관함수 그래프에서 lag 2에서 절단

위의 결과처럼 단순 AR or MA로 모형을 나누기엔 결정하기가 좀 힘들다.

이처럼 어떤 모형을 선택해야할 지는 쉽지 않은 문제이다.

$ARMA(p,q)$에서는 AR모형과 MA 모형을 혼합하여 모형을 식별하고 결정할 필요가 있다. 만약 모수가 많다면 설명력은 커질 것이다. 하지만 모형이 복잡하고 이해하기는 더 어려워진다.

그렇다고 모수가 너무 적으면 모형이 단순해서 이해력은 높아지나 설명력이 낮아질 수 밖에 없다. 그렇기에 항상 Trade-Off는 존재한다.

5) 적절한 ARIMA 모형 찾기

  • forecast package 에 내장된 auto.arima() 함수 이용
  • ARMIA 모형 찾기
1

auto.arima(Nile)

💻 출력결과

1
2
3
4
5
6
7
8
9
10

Series: kings$age
ARIMA(0,1,1)

Coefficients:
          ma1
      -0.7218
s.e.   0.1208

sigma^2 estimated as 236.2:  log likelihood=-170.06
AIC=344.13   AICc=344.44   BIC=347.56

💡 적절한 ARIMA모형은 ARIMA(1, 1, 1)이다 .

6) 예측

arima 결과를 활용한 forecast 예측

1
2
3
4
5
6

#arima 결과 1,1,1 대입
Nile.arima <- arima(Nile, order=c(1,1,1))
#arima 결과를 활용한 forecast 예측
Nile.forecast <- forecast(Nile.arima, h = 10)
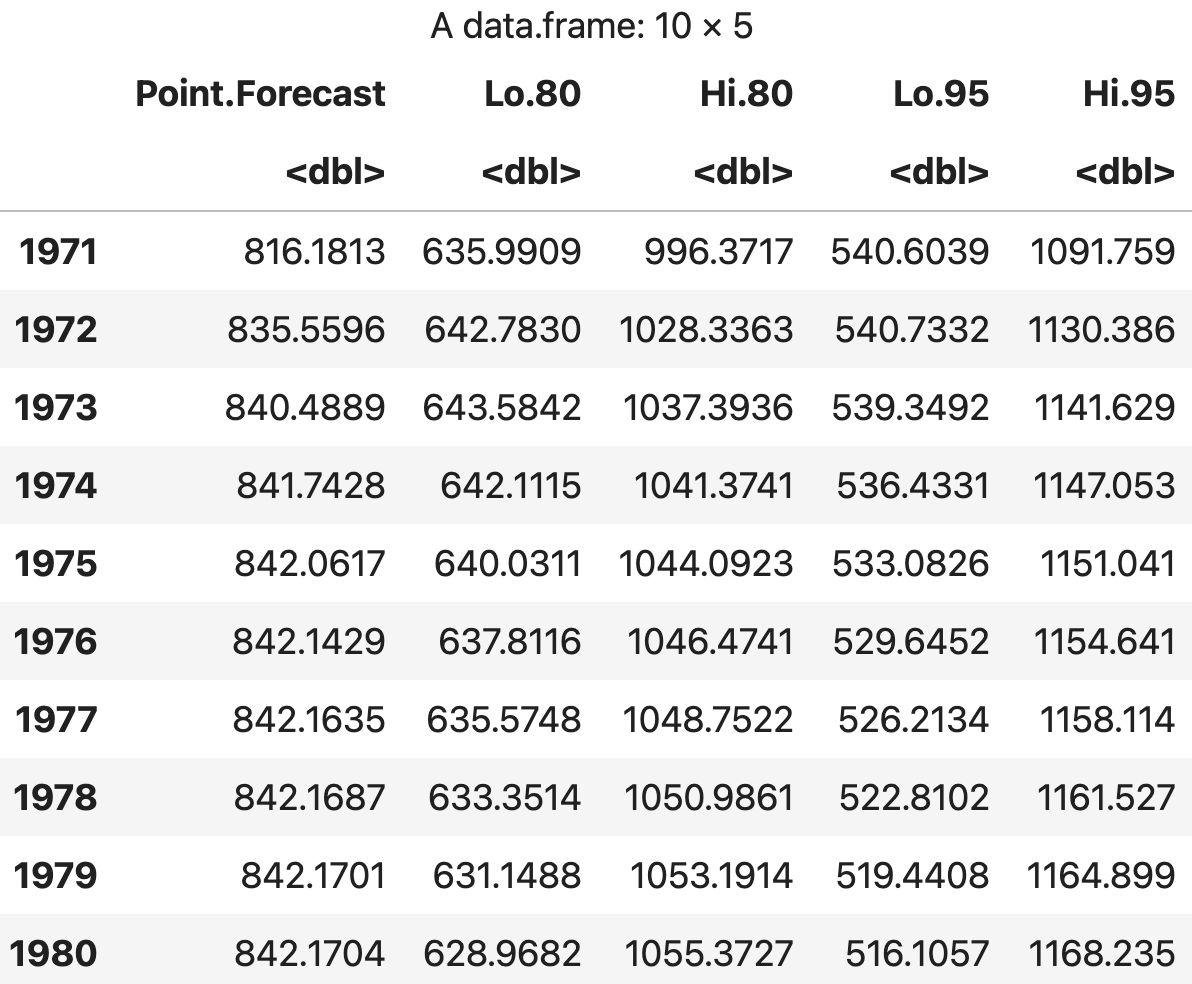
df <- data.frame(Nile.forecast)
df

💻 출력결과

/images/2022/1228/img_24.png

예측결과 시각화

  • 예측 결과를 시각화 하기
1

plot(Nile.forecast)

💻 출력결과

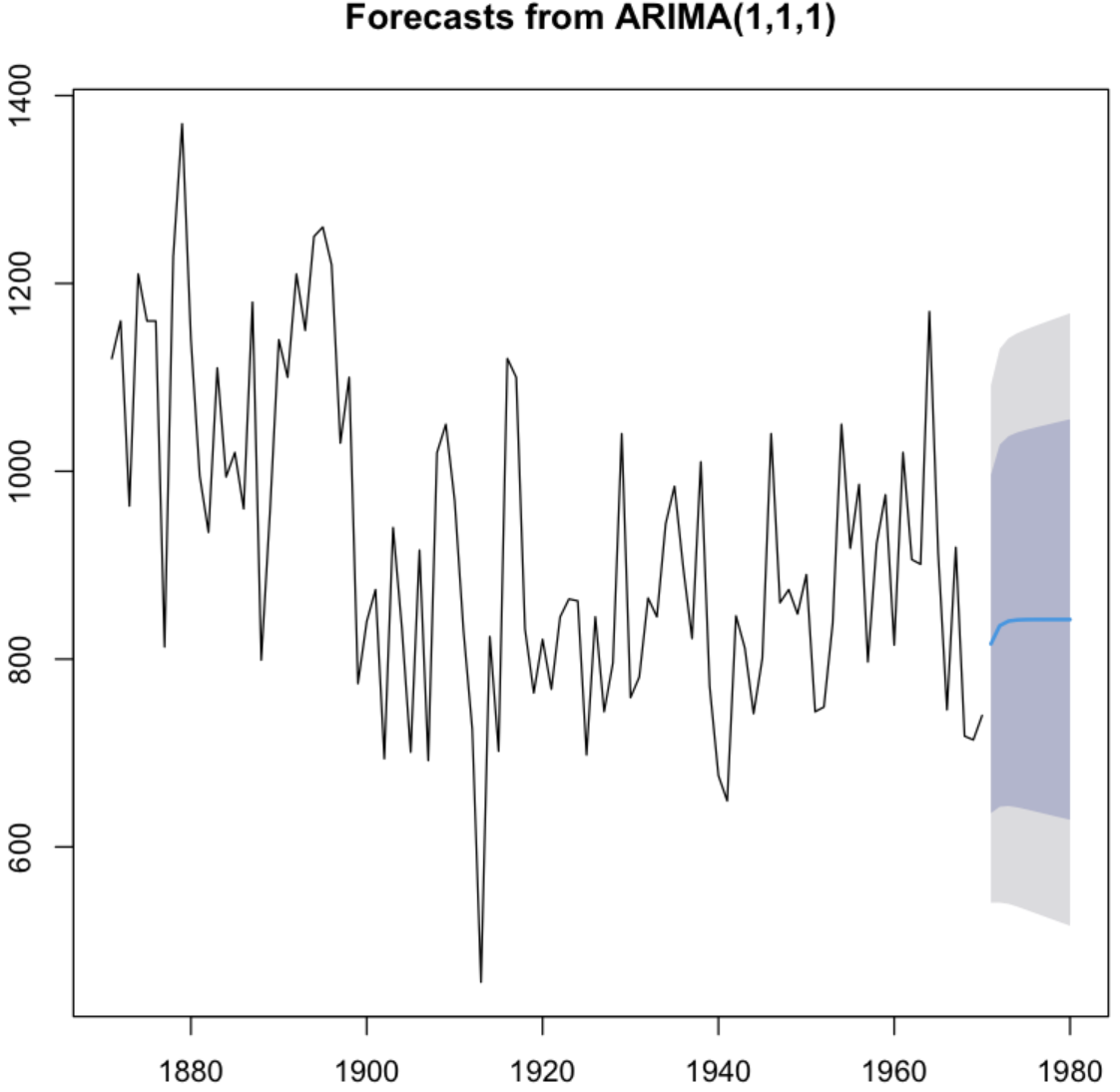
/images/2022/1228/img_25.png

💡 진한 파란선이 점추정과 같은 회귀선이고 가장 높은 옅은 파란 영역(80%)과 회색영역(95%)이 신뢰구간인 구간예측값이다.

R
This post is licensed under CC BY 4.0 by the author.