JAVA 재귀호출의 이해

#01. 재귀호출의 이해

💡 어느 한 컴퓨터공학과 학생이 유명한 교수님을 찾아가 물었다.
"재귀함수가 뭔가요?"
"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을 통달한 선인이 있었어.
마을 사람들은 모두 그 선인에게 수많은 질문을 했고, 모두 지혜롭게 대답해 주었지.
그의 답은 대부분 옳았다고 하네.
그런데 어느날, 그 선인에게 한 선비가 찾아와서 물었어.
"재귀함수가 뭔가요?"
"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을 통달한 선인이 있었어.
마을 사람들은 모두 그 선인에게 수많은 질문을 했고, 모두 지혜롭게 대답해 주었지.
그의 답은 대부분 옳았다고 하네.
그런데 어느날, 그 선인에게 한 선비가 찾아와서 물었어.
"재귀함수가 뭔가요?"
"잘 들어보게. ..."

위의 유머에서의 두 가지 포인트는

1. 계속해서 반복되는 내용이 등장한다.
2. 끝도 없이 계속된다.

재귀호출은 마지막에 종료 조건을 명시하지 않는다면 무한루프에 빠지게 된다.

그러므로 재귀호출을 구현할 때 가장 먼저 처리해야 할 것은 종료조건을 명시하는 것이다.

#02. 재귀호출 예제

1) 팩토리얼 구하기

팩토리얼은 해당 1부터 해당 값까지의 순차적인 곱을 의미한다.

📗 Ex01_팩토리얼_반복문.java

public class Ex01_팩토리얼_반복문 {
    public static void main(String[] args) {
        int n = 5;
        int result = 1;
        for (int i = 1; i <= n; i++) {
            result *= i;
        }
        System.out.println(result);
    }
}

재귀호출을 통한 구현

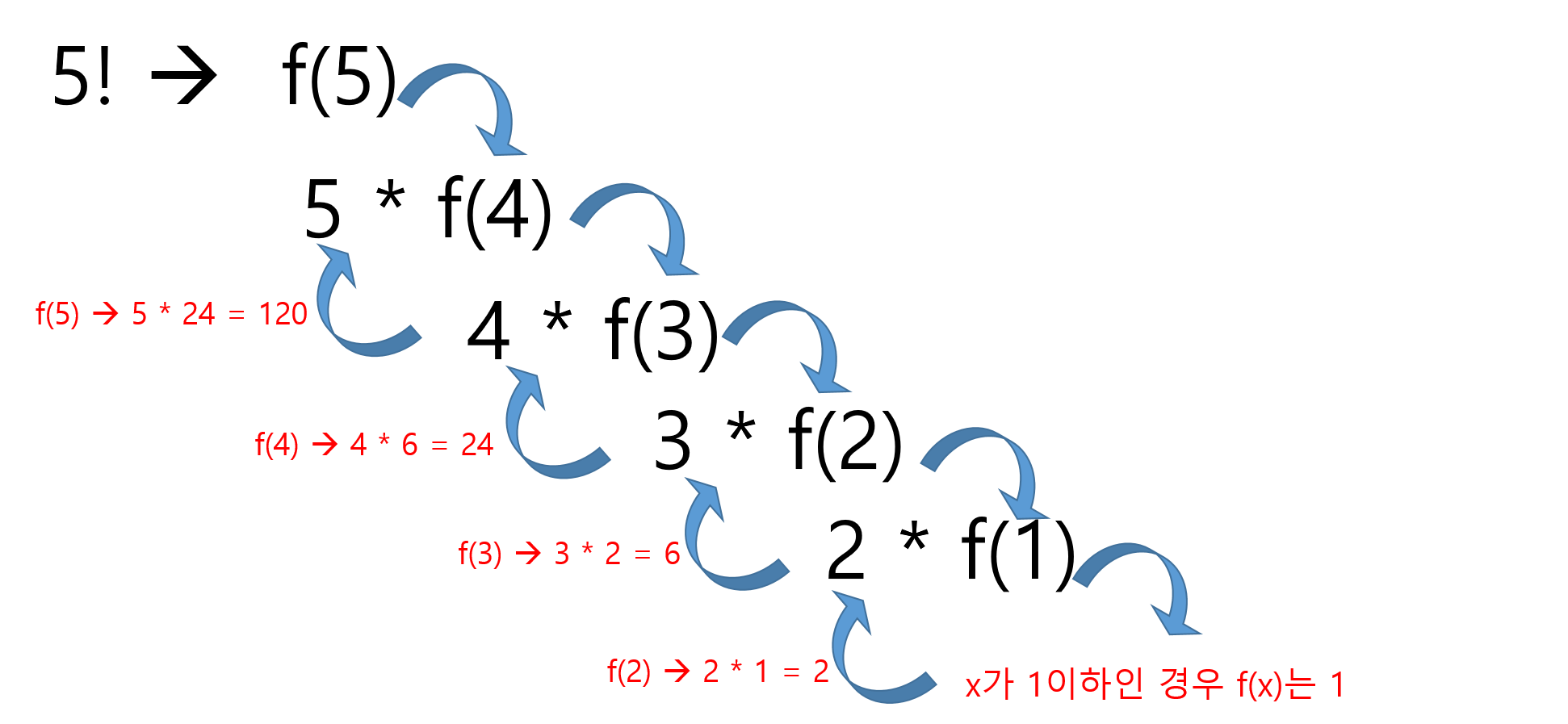
팩토리얼의 수식을 분석해 본다면 다음과 같이 정의할 수 있다.

\[f(x) = x \times f(x-1) \\ (단, x가 1 이하인 경우 1)\]

팩토리얼의 경우 주어진 값 부터 $1$ 까지만 $1$ 씩 감소하면서 곱하는 것이므로 조건값이 $1$ 보다 작거나 같다면 $1$ 을 리턴해야 한다. (곱셈에서의 $1$ 은 무의미하기 때문)

if (max <= 1) {
    return 1;
}

📗 Ex02_팩토리얼_재귀호출.java

public class Ex02_팩토리얼_재귀호출 {
    public static void main(String[] args) {
        // 팩토리얼을 구하기 위한 메서드 호출
        long result = factorial(5);
        // 결과 출력
        System.out.println(result);
    }

    // 팩토리얼을 리턴하는 재귀 메소드
    public static int factorial(int n) {
        if (n == 1) {
            return 1;
        }
        return n * factorial(n - 1);
    }
}

2) 총 합 구하기

양의 정수 $1$ 부터 $n$ 까지의 총 합을 구하는 기능을 재귀함수로 구현하시오.

$n$부터 $1$ 씩 감소하면서 합산을 하고 $1$ 이 되는 순간 더 이상 진행하지 않고 종료해야 한다.

예를 들어 $n$ 이 $5$ 일 때, $5 + 4 + 3 + 2 + 1$ 이 되어야 한다.

이를 수식으로 표현하면 다음과 같다.

\[\begin{align} f(1) &= 1 \\ f(n) &= n + f(n-1) \end{align}\]

재귀 호출의 종료조건은 $n$ 이 $1$ 이 되는 경우이다.

if (n == 1) {
    return 1;
}

📗 Ex03_합계구하기.java

public class Ex03_합계구하기 {
    public static void main(String[] args) {
        // sum을 호출하여 리턴값을 a에 저장
        int a = sum(10);

        // a의 값을 출력
        System.out.println(a);
    }

    // 1부터 n까지의 합을 구하는 재귀 메소드
    public static int sum(int n) {
        if (n == 1) {
            return 1;
        }
        return n + sum(n - 1);
    }
}

#03. 구구단

구구단 $7$ 단의 결과를 출력하는 재귀 호출 메서드

📗 Ex04_구구단.java

public class Ex04_구구단 {
    public static void main(String[] args) {
        gugudan(1);
    }

    // 파라미터값에 대한 구구단 7단을 출력하는 재귀 메서드
    public static void gugudan(int n) {
        if (n > 9) {
            return;
        }

        System.out.printf("%d x %d = %d\n", 7, n, 7*n);
        gugudan(n+1);
    }
}

#04. 피보나치 수

피보나치 수는 다음과 같은 초기값 및 점화식으로 정의되는 수열이다.

\[\begin{align} f(0) &= 0 \\ f(1) &= 1 \\ f(n) &= f(n-1) + f(n-2) \end{align}\]

$n$ 값이 $2$ 부터 증가하는 동안 다음과 같이 표현된다.

\[\begin{align} f(2) &= f(1) + f(0) = 1 + 0 = 1 \\ f(3) &= f(2) + f(1) = 1 + 1 = 2 \\ f(4) &= f(3) + f(2) = 2 + 1 = 3 \\ f(5) &= f(4) + f(3) = 3 + 2 = 5 \\ f(6) &= f(5) + f(4) = 5 + 3 = 8 \end{align}\]

📗 Ex05_피보나치수.java

public class Ex05_피보나치수 {
    public static void main(String[] args) {
        for (int i = 1; i<=10; i++) {
            System.out.printf("%d에 대한 피보나치 수는 %d\n", i, fibonacci(i));
        }
    }

    // 파라미터값 n에 대한 피보나치 수를 모두 출력하는 재귀 메서드
    public static int fibonacci(int n) {
        if (n <= 1) {
            return n;
        } else {
            return fibonacci(n-2) + fibonacci(n-1);
        }
    }
}