#01. 시계열 분석 개요

1) 시계열 자료

시계열 자료 개요

시간의 흐름에 따라 관찰된 값들
시계열 데이터의 분석을통해 미래의 값을 예측하고 경향, 주기, 계절성 등을 파악하여 활용한다.

시계열 자료의 종류

비정상성 시계열 자료 - 시계열 분석을 실시할 때 다루기 어려운 자료로 대부분의 시계열자료.
정상성 시계열 자료- 비정상 시계열을 핸들링해 다루기 쉬운 시계열 자료로 변환한 자료

2) 정상성 🌟

평균이 일정할 경우

모든 시점에 대해 일정한 평균을 가진다 .
평균이 일정하지 않은 시계열은 차분 (difference )을 통해 정상화할 수 있다 .

분산이 일정

분산도 시점에 의존하지 않고 일정해야 한다 .
분산이 일정하지 않을 경우 변환(Transformation )을 통해 정상화할 수 있다.

공분산도 단지 시차에만 의존, 실제 특정 시점 t, s 에는 의존하지 않는다.

약한의미의 정상성

모든 시점에 평균일정, 시점과 분산 독립, 공분산은 시차에만 의존

비정상→정상 : 변환(transformation), 차분(difference)

변환 : 분산이 일정하지 않은 비정상 시계열
차분(t1-t0) : 평균이 일정하지 않은 비정상 시계열
일반차분 (regular difference) : 바로 전 시점의 자료를 빼는 방법이다 .
계절차분 (seasonal difference) ：여러 시점 전의 자료를 빼는 것 방법 , 주로 계절성을 갖는 자료를 정상화 하는데 사용한다 .

#02. 정상시계열

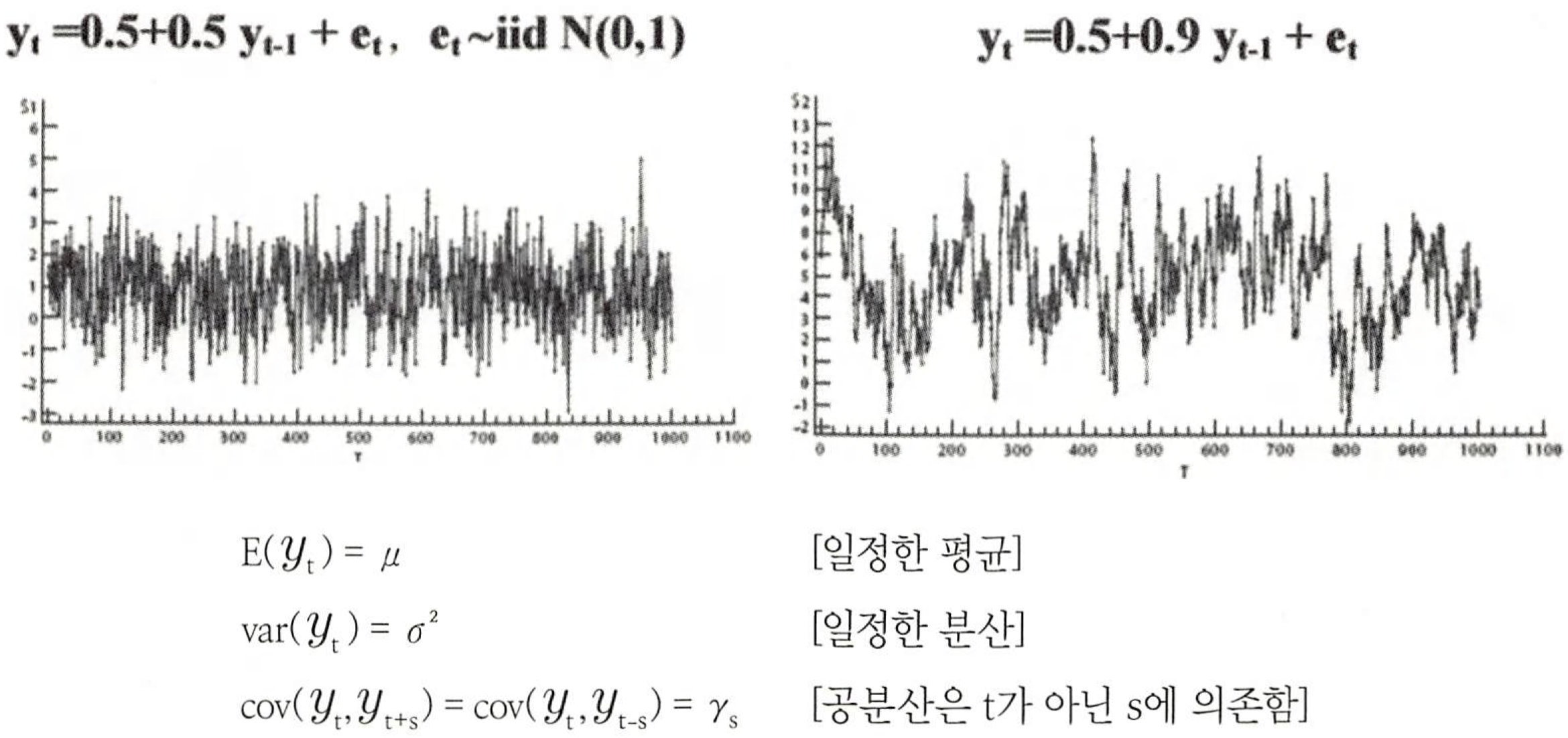
정상 시계열은 어떤 시점에서 평균과 분산 그리고 특정한 시차의 길이를 갖는 자기공분산을 측정하더라도 동일한 값을 갖는다.
정상 시계열은 항상 그 평균값으로 회귀하려는 경향이 있으며，그 평균값 주변에서의 변동은 대체로 일정한 폭을 갖는다.
정상 시계열이 아닌 경우 특정 기간의 시계열 자료로부터 얻은 정보를 다른 시기로 일반화 할 수 없다.

/images/posts/2022/1228/img_0.png

#03. 시계열 분석 모형

1) 분석방법 종류

분석방법에 따른 구분

이름	태그	설명
수학적 이론 모형	Box-Jenkins, 회귀분석(계량경제)
직관적 방법	시계열 분해법, 지수평활법	시간에 따른 변동이 느린 데이터 분석에 활용
장기 예측	회귀분석방법
단기 예측	Box-Jenkins, 시계열 분해법, 지수평활법

자료 형태에 따른 구분

이름	태그	설명
일변량 시계열분석	Box-Jenkins(ARMA), 시계열 분해법, 지수 평활법	시간 (t)을 설명변수로 한 회귀모형주가，소매물가지수 등 하나의 변수에 관심을 갖는 경우의 시계열분석
다중 시계열분석	다변량 ARIMA, 개입분석, 계량경제 모형, 상태공간 분석, 전이함수 모형	여러개의 시간(t)에 따른 변수들을 활용하는 시계열 분석

3) 이동평균모형(MA모형) 🧨

이동평균법의 개념

과거로부터 현재까지의 시계열 자료를 대상으로 일정기간별 이동평균을 계산하고，이들의 추세를 파악하여 다음 기간을 예측하는 방법
시계열 자료에서 계절변동과 불규칙변동을 제거하여 추세변동과 순환변동만 가진 시계열로 변환하는 방법으로도 사용됨

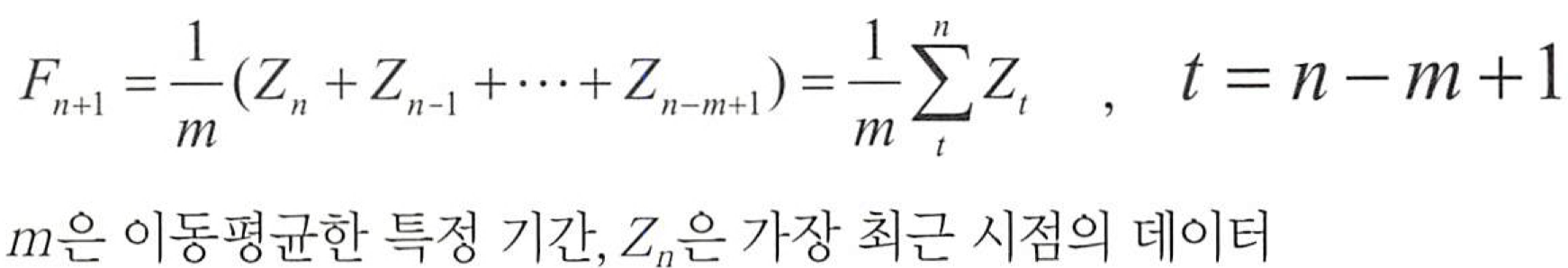
/images/posts/2022/1228/img_1.png

n 개의 시계열 데이터를 m 기간으로 이동평균하면 n-m+1 개의 이동평균 데이터가 생성된다.

이동평균법의 특징

간단하고 쉽게 미래를 예측
자료의 수가 많고 안정된 패턴을 보이는 경우 예측의 품질이 높음
특정 기간 안에 속하는 시계열에 대해서는 동일한 가중치를 부여함
일반적으로 시계열 자료에 뚜렷한 추세가 있거나 불규칙변동이 심하지 않은 경우에는 짧은 기간 (m의 개수를 적음)의 평균을 사용, 반대로 불규칙변동이 심한 경우 긴 기간 (m의 개수가 많음) 의 평균을사용함
이동평균법에서 가장 중요한 것은 적절한 기간을 사용하는 것. 즉, 적절한 n 의 개수를 결정 하는 것임.

4) 지수평활법 🧨

지수평활법의 개념

일정기간의 평균을 이용하는 이동평균법과 달리 모든 시계열 자료를 사용하여 평균을 구하며, 시간의 흐름에 따라 최근 시계열에 더 많은 가중치를 부여하여 미래를 예측하는 방법.

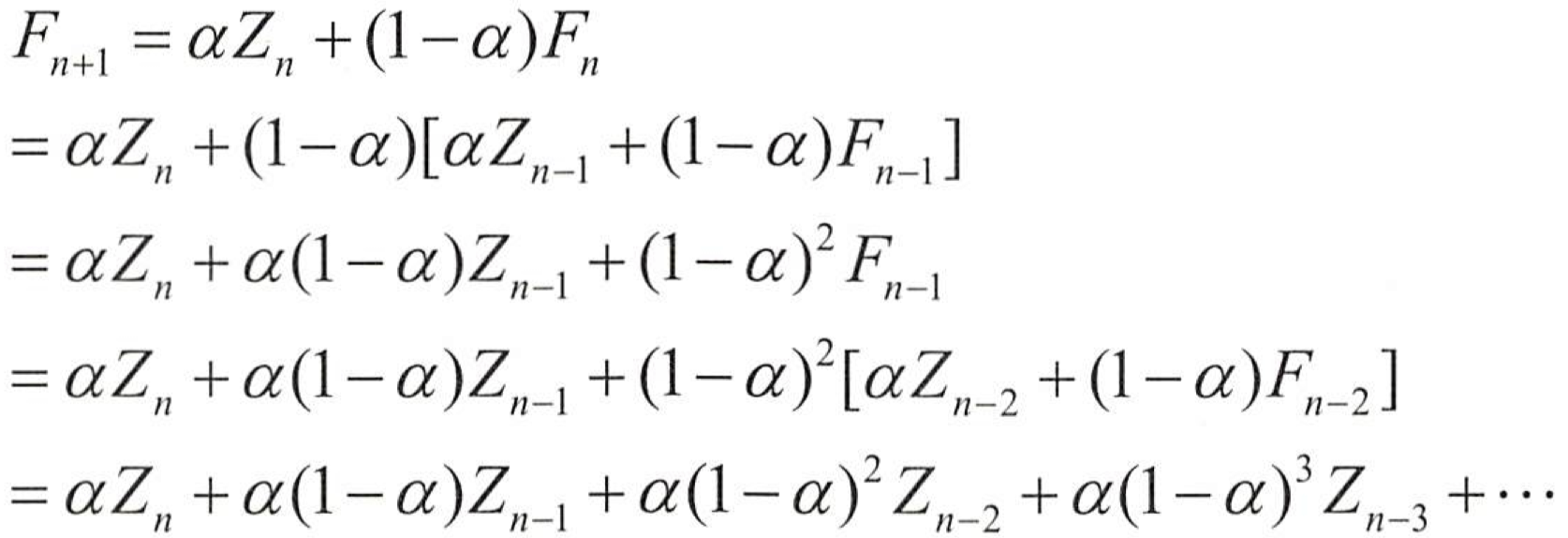
/images/posts/2022/1228/img_2.png

여기서 Fn+1은 n 시점 다음의 예측값，a 는 지수평활계수，Z n은 n 시점의 관측값.
지수평활 계수가 과거로 갈수록 지수형태로 감소하는 형태

지수평활법의 특징

단기간에 발생하는 불규칙변동을 평활하는 방법
자료의 수가 많고，안정된 패턴을 보이는 경우일수록 예측 품질이 높음
지수평활법에서 가중치의 역할을 하는 것은 지수평활계수 (a) 이며 , 불규칙변동이 큰 시계열의 경우 지수평활계수는 작은 값을，불규칙변동이 작은 시계열의 경우 , 큰 값의 지수평활계수를 적용함
지수평활계수는 예측오차(실제 관측치와 예측치 사이의 잔차제곱합)를 비교하여 예측오차가 가장 작은 값을 선택하는 것이 바람직함
지수평활계수는 과거로 갈수록 지속적으로 감소함
지수평활법은 불규칙변동의 영향을 제거하는 효과가 있으며，중기 예측 이상에 주로 사용됨 (단，단순지수 평활법의 경우，장기추세나 계절변동이 포함된 시계열의 예측에는 적합하지 않음)

#04. 시계열 모형 🌟

1) 자기회귀모형(AR모형)

p시점 전의 자료가 현재 자료에 영향을 주는 자귀회귀모형을 AR(p) 모형이라 함

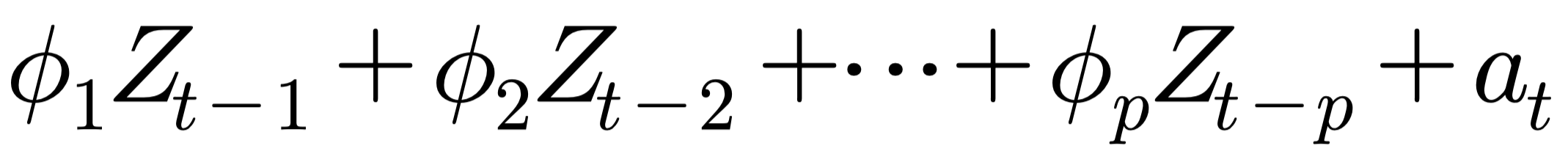
/images/posts/2022/1228/img_3.png

$a_t$ : white noise process(백색잡음과정)
자귀회귀모형 판단 조건 : 자기상관함수(ACF) 빠르게 감소하고 부분자기상관함수(PACF)는 어느 시점에 절단점 갖음

2) 이동평균모형(MA모형)

유한한 개수의 백색잡음의 결합. 항상 정상성 만족

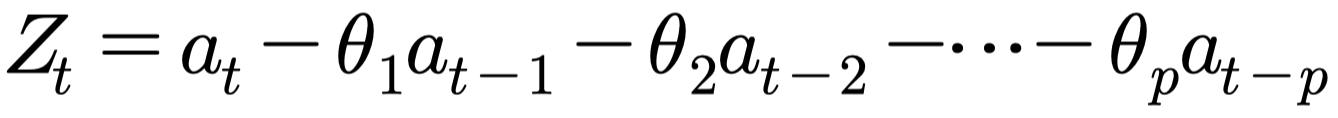
/images/posts/2022/1228/img_4.png

ACF에서 절단점 갖고 PACF가 빠르게 감소

3) 자기회귀누적이동평균모형(ARIMA(p,d,q)모형) 🌟🌟🌟

가장 일반적인 모형
비정상시계열 모형
차분이나 변환을 통해 AR/MA/ARMA 모형으로 정상화 가능
p는 AR, q는 MA와 관련있는 차수로 ARIMA에서 ARMA로 정상화할 때 차분한 횟수 의미
d=0 이면 ARMA(p,q) 모형이라 부르고，이모형은 정상성을 만족한다 .(ARM A(0,0) 일 경우 정상 화가 불필요하다)
p=0 이면 IMA(d, q) 모형이라고 부르고 , d번 차분하면 MA(q) 모형을 따른다 .
q=0 이면 ARI(p, d) 모형이라 부르며, d 번 차분한 시계열이 AR(p) 모형을 따른다 .

예시

ARIMA(0, 1, 1)의 경우에는 1차분 후 MA(1) 활용
ARIMA(1, 1, 0)의 경우에는 1차 분 후 AR(1) 활용

4) 분해 시계열

시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
회귀분석적 방법 주로 사용
시계열 구성 요소 🌟
1. 추세요인(trend factor) : 자료가 어떤 특정한 형태를 취할 때
2. 계절요인(seasonal factor) : 고정된 주기에 따라 자료가 변화
3. 순환요인(cyclical factor) : 알려지지 않은 주기를 갖고 자료가 변화
4. 불규칙요인(irregular factor) : 회귀분석에서 오차에 해당하는 요인
분해시계열분석법에서는 각 구성요인을 정확히 분리하는 것이 중요
요인 정확히 분리하기 쉽지 않으며 이론적 약점 존재 but 많이 사용됨

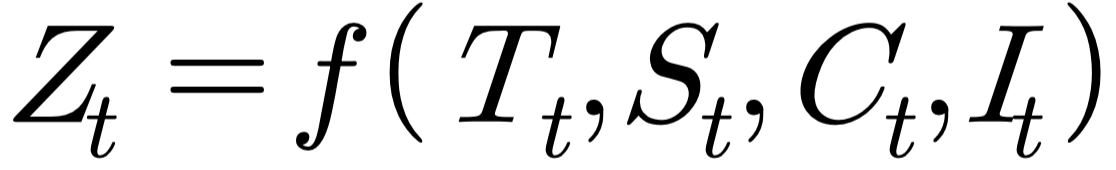
/images/posts/2022/1228/img_5.png

#05. 시계열 분석 R 실습 (1)

1) 필요한 패키지 및 데이터 가져오기

패키지 로드

REPO_URL <- "https://cran.seoul.go.kr/"

if (!require("tseries")) install.packages("tseries", repos=REPO_URL)
if (!require("forecast")) install.packages("forecast", repos=REPO_URL)
if (!require("TTR")) install.packages("TTR", repos=REPO_URL)

library(tseries)
library(forecast)
library(TTR)

데이터 가져오기

kings <- read.csv("http://itpaper.co.kr/demo/r/kings.csv", stringsAsFactors=F, fileEncoding="utf-8")
head(kings)

💻 출력결과

/images/posts/2022/1228/img_6.png

2) 시계열 그래프 그리기

plot.ts() 함수를 사용하여 시계열 데이터를 선 그래프 형태로 표현한다.

숫자로만 구성된 변수를 파라미터로 전달하게 되는데 이 데이터들은 y축에 해당하고 x축은 시간의 흐름(time)으로 자동 설정된다.

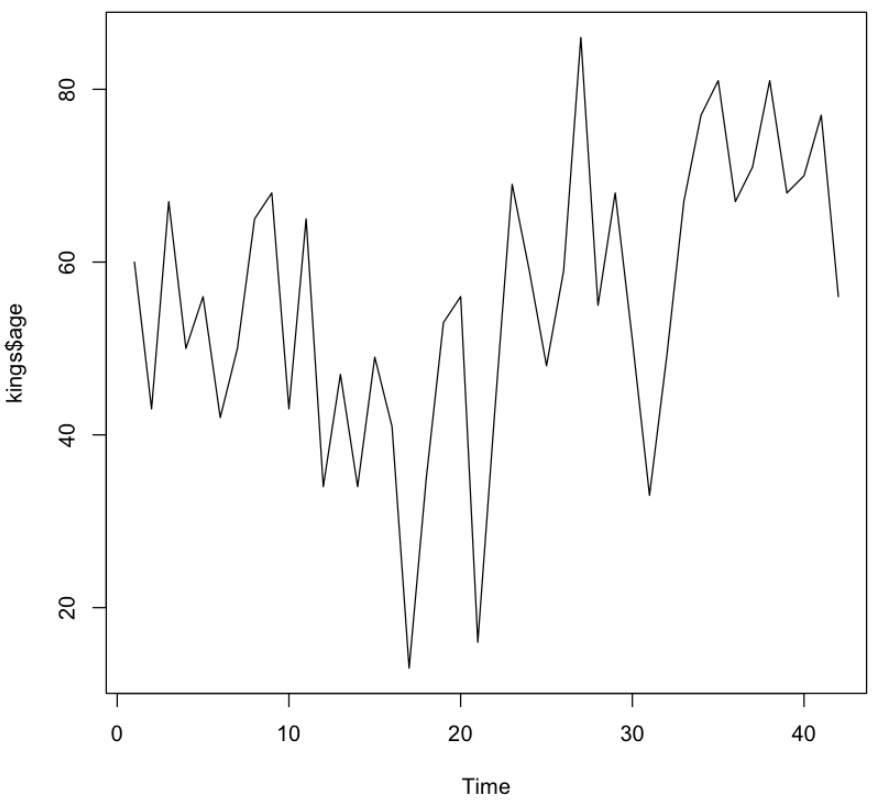
기본 형태의 시계열 그래프

plot.ts(kings$age)

💻 출력결과

/images/posts/2022/1228/img_7.png

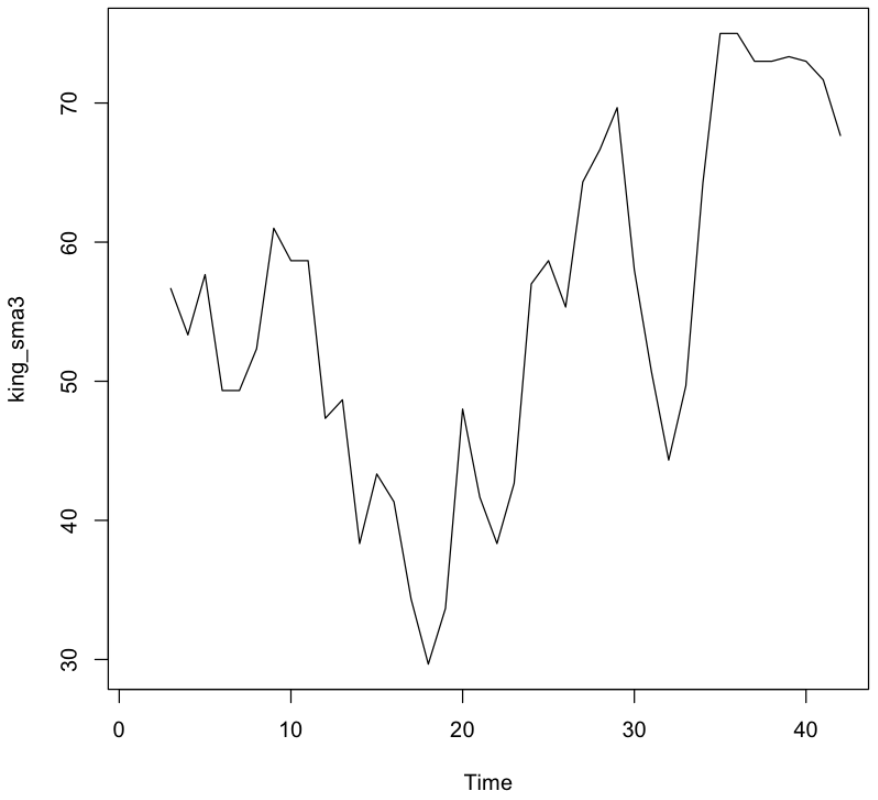
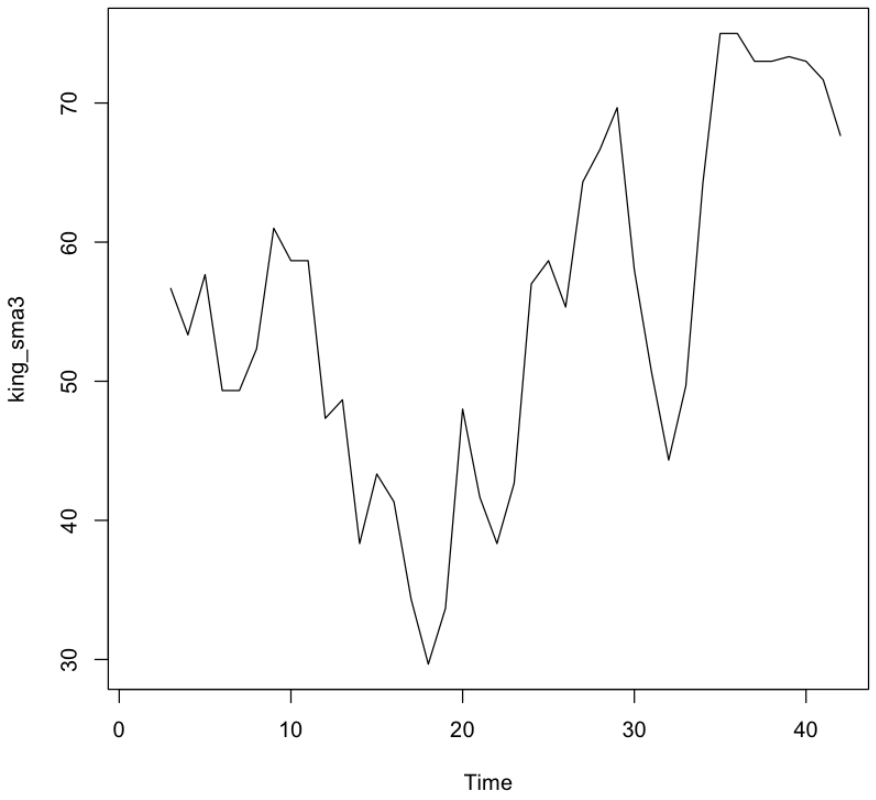
3년마다 평균을 내서 그래프를 부드럽게 표현

king_sma3 <- SMA(kings$age, n=3)
plot.ts(king_sma3)

💻 출력결과

/images/posts/2022/1228/img_8.png

8년마다 평균을 내서 그래프를 부드럽게 표현

king_sma8 <- SMA(kings$age, n=8)
plot.ts(king_sma3)

💻 출력결과

/images/posts/2022/1228/img_9.png

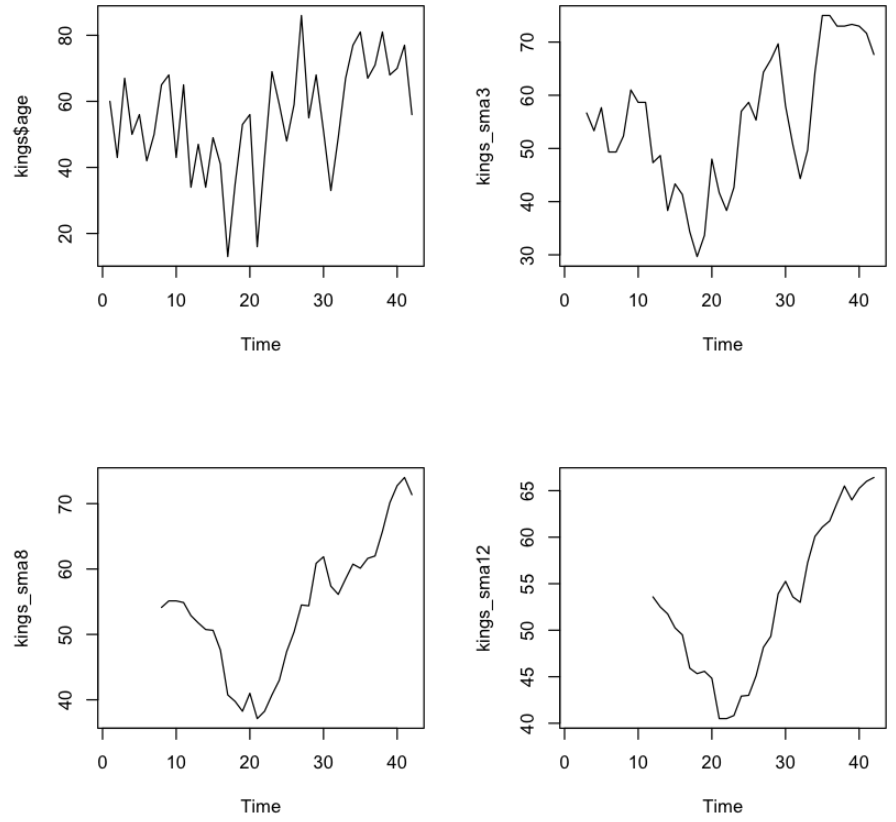
이동 평균 한번에 보기

kings_sma3 <- SMA(kings$age, n = 3)
kings_sma8 <- SMA(kings$age, n = 8)
kings_sma12 <- SMA(kings$age, n = 12)

par(mfrow = c(2,2))

plot.ts(kings$age)
plot.ts(kings_sma3)
plot.ts(kings_sma8)
plot.ts(kings_sma12)

💻 출력결과

/images/posts/2022/1228/img_10.png

3) ARIMA 모델 적용

데이터 정상화

ARIMA 모델은 정상성 시계열에 한해 사용한다 .

비정상 시계열 자료는 차분해 정상성으로 만족하는 조건의 시계열로 바꿔준다 .
이전 그래프에서 평균이 시간에 따라 일정치 않은 모습을 보이므로 비정상시계열이다 .

따라서 차분을 진행한다 .

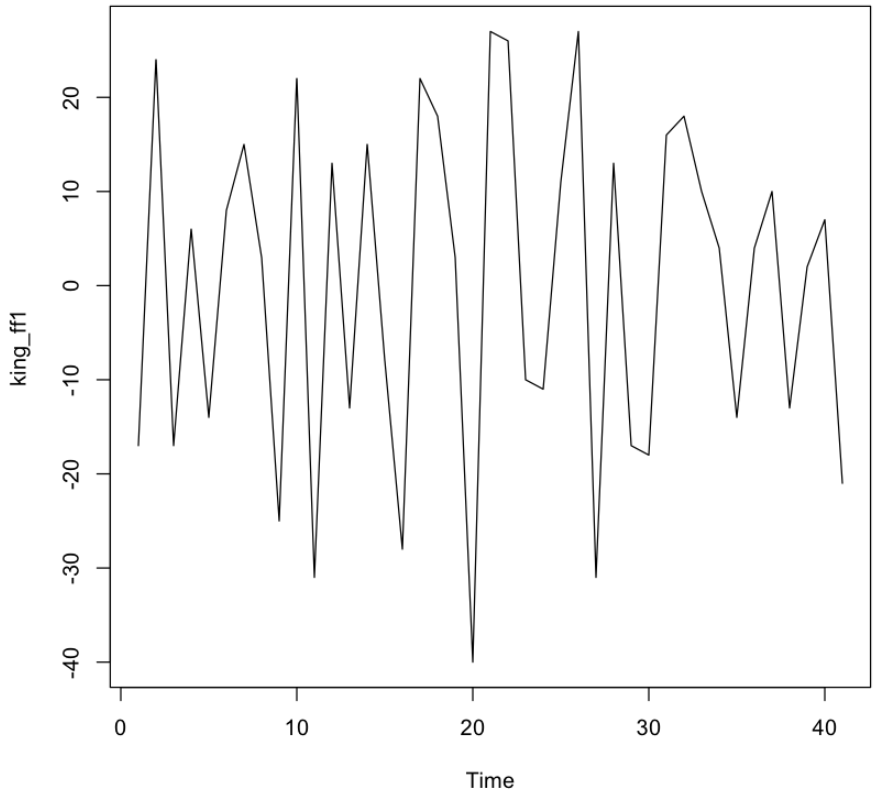
1차 차분 결과에서 평균과 분산이 시간에 따라 의존하지 않음을 확인한다 .
ARIMA(p, 1, q)모델이며 차분을 1번 해야 정상성을 만족한다.
1차 차분 진행

king_ff1 <- diff(kings$age, differences=1)
plot.ts(king_ff1)

💻 출력결과

/images/posts/2022/1228/img_11.png

ACF와 PACF 를 통한 적합한 ARIMA 모델 결정

ACF

acf(king_ff1, lag.max=20)
acf(king_ff1, lag.max=20, plot=FALSE)

💻 출력결과

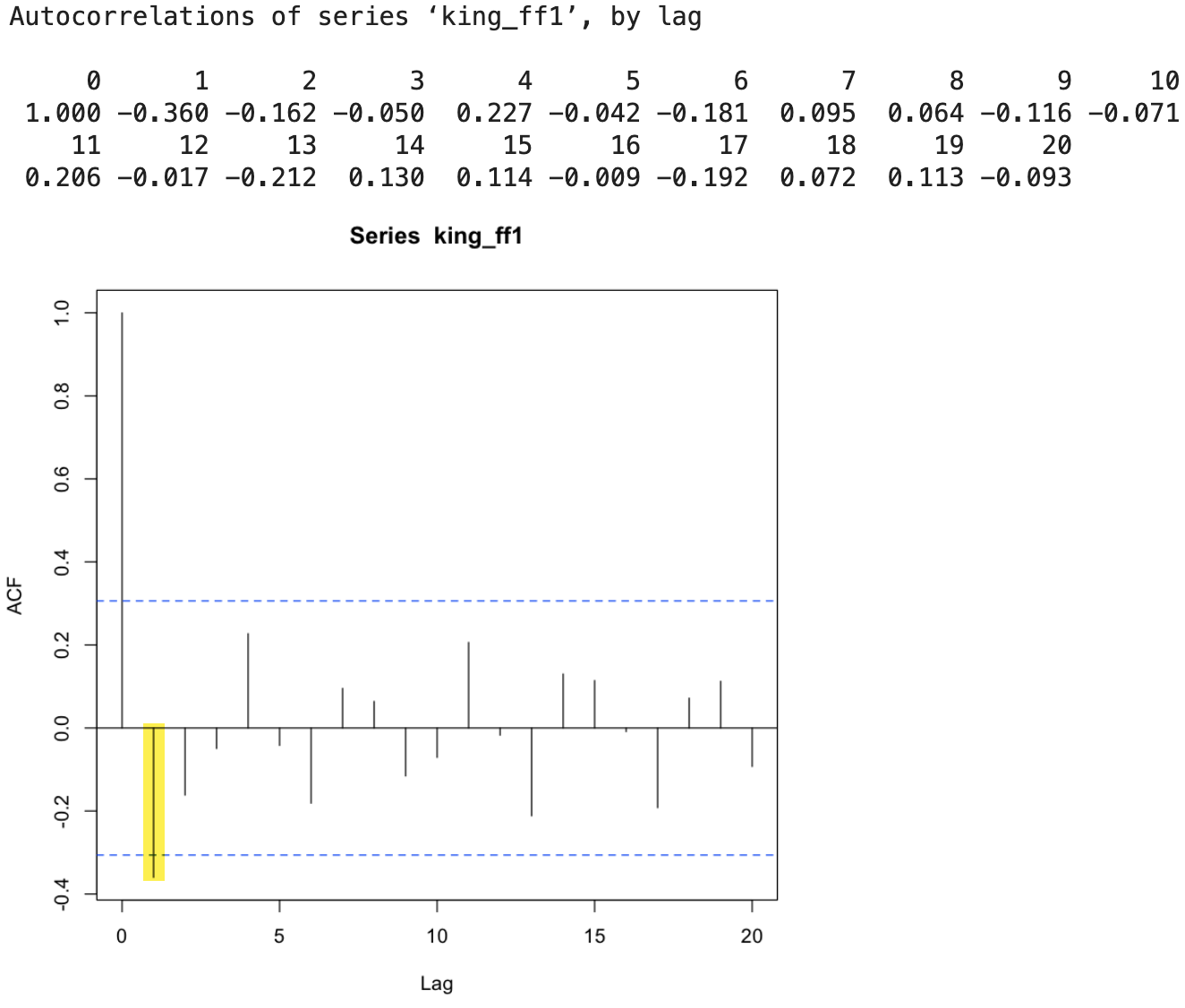
/images/posts/2022/1228/img_12.png

💡 lag 는 0부터 값을 갖는데，너무 많은 구간을 설정하면 그래프를 보고 판단하기 어렵다. * ACF값이 lag 1인 지점 빼고는 모두 점선 구간 안에 있고 , 나머지는 구간 안에 있다.

PCAF

pacf(king_ff1, lag.max=20)
pacf(king_ff1, lag.max=20, plot=FALSE)

💻 출력결과

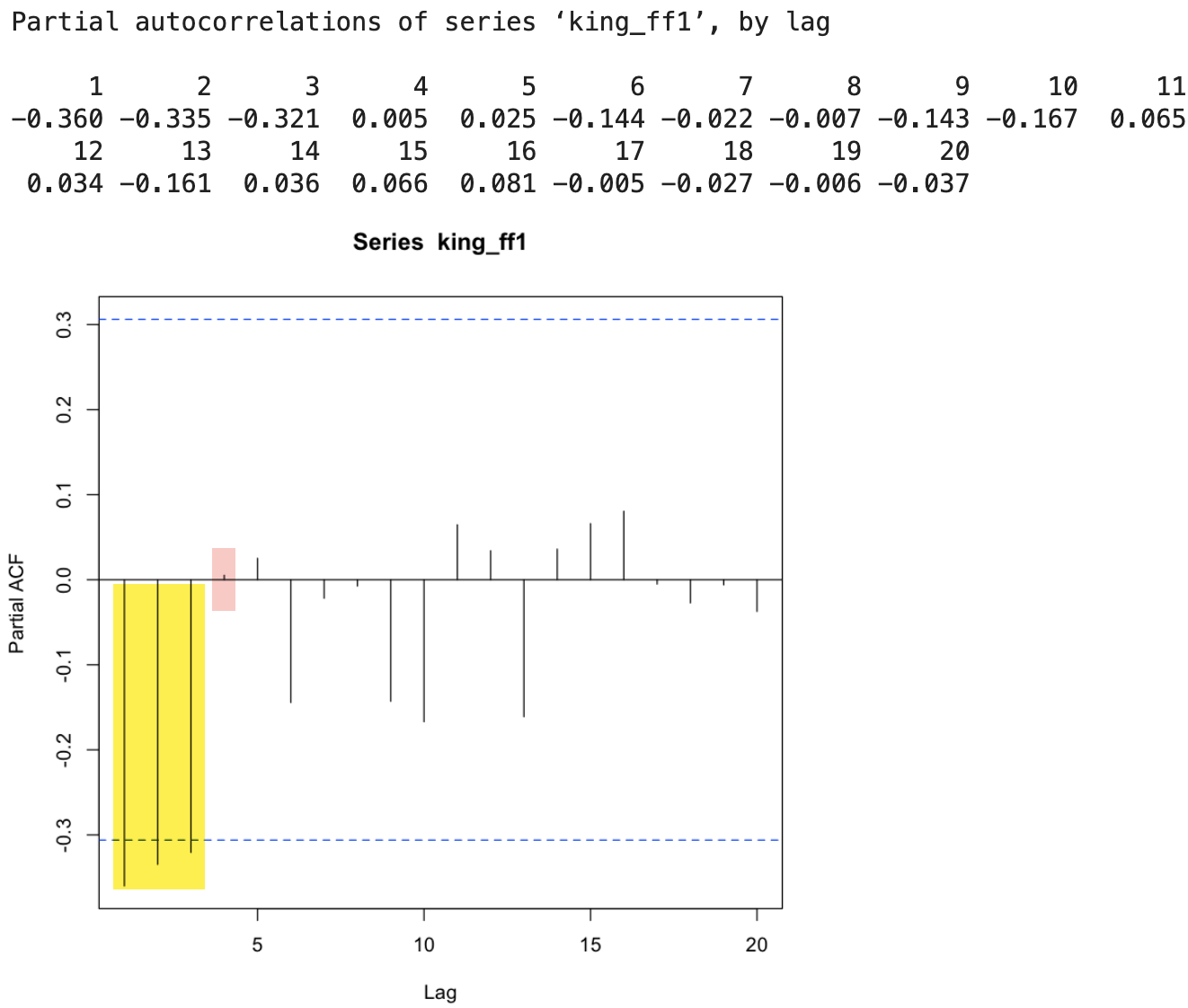
/images/posts/2022/1228/img_13.png

💡 PACF - PACF 값이 lag 1, 2, 3에서 점선 구간을 초과하고 음의 값을 가지며 절단점이 lag 4 이다 .

4) 종합

ARMA 후보들이 생성
ARMA(3, 0) 모델 : PACF 값이 lag4 에서 절단점을 가짐. → ARMA(3)모형
ARMA(0, 1) 모델 : ACF 값이 lag2 에서 절단점을 가짐 → MA(1)모형
ARMA(p，q) 모델 : 그래서 AR모형과 MA모형을 혼합

5) 적절한 ARIMA 모형 찾기

forecast package 에 내장된 auto.arima() 함수 이용
ARMIA 모형 찾기

auto.arima(kings$age)

💻 출력결과

Series: kings$age 
ARIMA(0,1,1) 

Coefficients:
          ma1
      -0.7218
s.e.   0.1208

sigma^2 estimated as 236.2:  log likelihood=-170.06
AIC=344.13   AICc=344.44   BIC=347.56

💡 영국 왕의 사망 나이 데이터의 적절한 ARIMA모형은 ARIMA(0, 1, 1)이다 .

6) 예측

arima 결과를 활용한 forecast 예측

42 명의 영국왕 중에서 마지막 왕의 사망시 나이는 56 세
43 번째에서 52번째 왕까지 10명의 왕의 사망시 나이를 예측한 결과 67.75살로 추정된다 .
5 명 정도만 예측하고 싶다면，옵션에 h=5 를 입력한다 .
신뢰 구간은 80%~95% 사이
시계열 분석을 통한 영국 왕들의 사망시 나이 예측

king_arima <- arima(kings$age, order=c(0, 1, 1))
king_forecasts <- forecast(king_arima)
df <- data.frame(king_forecasts)
df

💻 출력결과

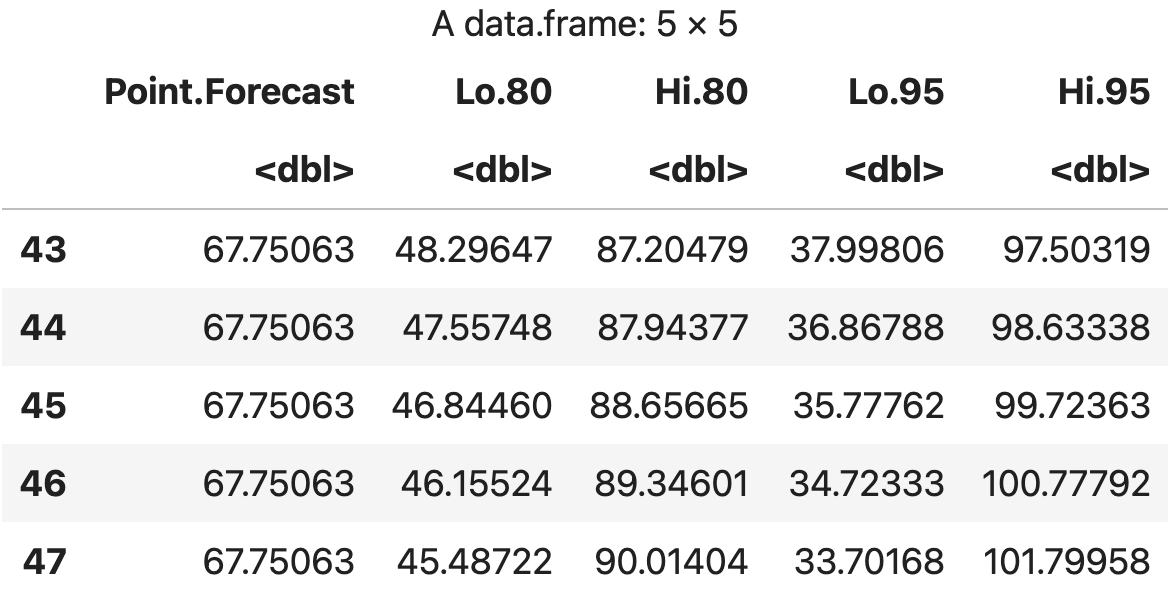
/images/posts/2022/1228/img_14.png

예측결과 시각화

plot(king_forecasts)

💻 출력결과

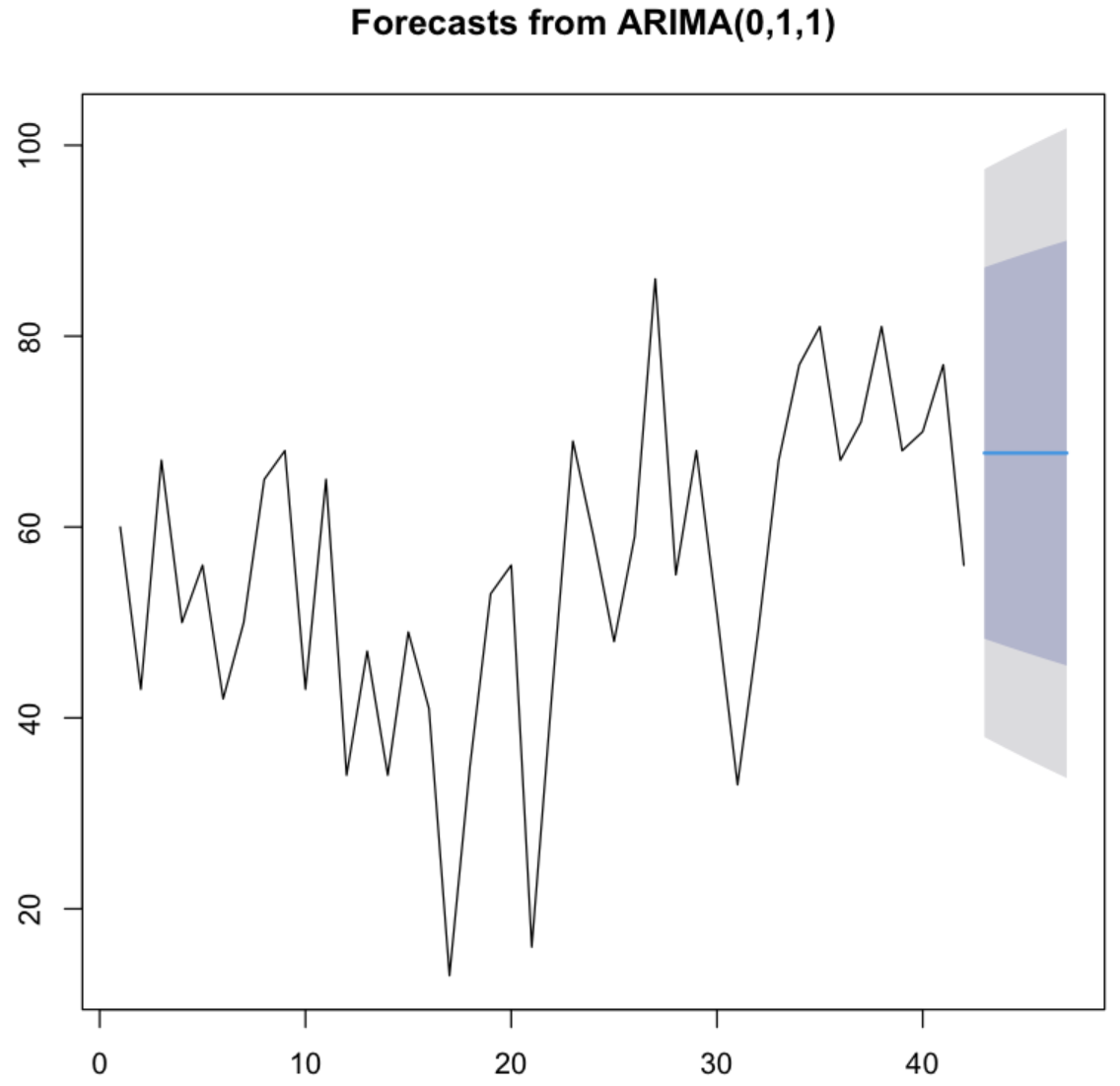
/images/posts/2022/1228/img_15.png

💡 진한 파란선이 점추정과 같은 회귀선이고 가장 높은 옅은 파란 영역(80%)과 회색영역(95%)이 신뢰구간인 구간예측값이다.

#06. 시계열 분석 R 실습 (2)

Nile 은 나일강 연간 유입량에 관한 데이터로서 R에 기본 내장되어 있다.

1) 데이터 가져오기

데이터 가져오기

df <- data.frame(Nile)
head(df)

💻 출력결과

/images/posts/2022/1228/img_16.png

2) 시계열 그래프 그리기

나일강 데이터를 먼저 살펴보면 규칙적인 계절성이 띄는 것 같아 보이지 않는다.

하지만, 평균이 변화하는 추세는 약간 보이는 듯 하다. 그렇기에 정상성을 만족하지 못한다.

기본 형태의 시계열 그래프

기본 형태의 시계열 그래프 그리기

plot.ts(Nile)

💻 출력결과

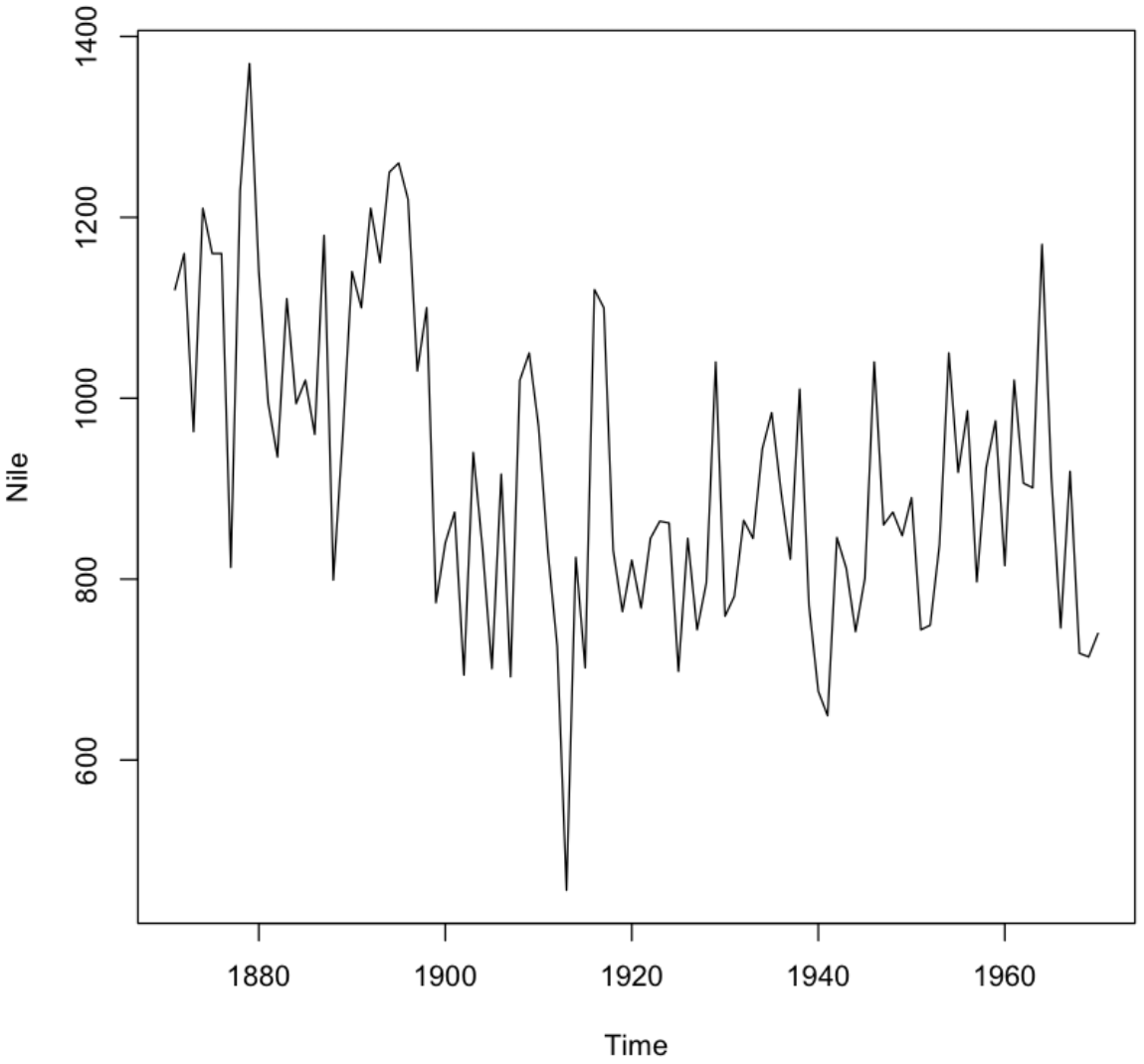
/images/posts/2022/1228/img_17.png

3) ARIMA 모델 적용

데이터 정상화

R에서 차분은 diff함수를 통해서 정할 수 있다. diff(ts, differences = d-횟수)를 사용하면, 원하는 d만큼 차분이 가능하다.

1차 차분 진행

Nile.diff_1 <- diff(Nile, differences = 1)
plot(Nile.diff_1)

💻 출력결과

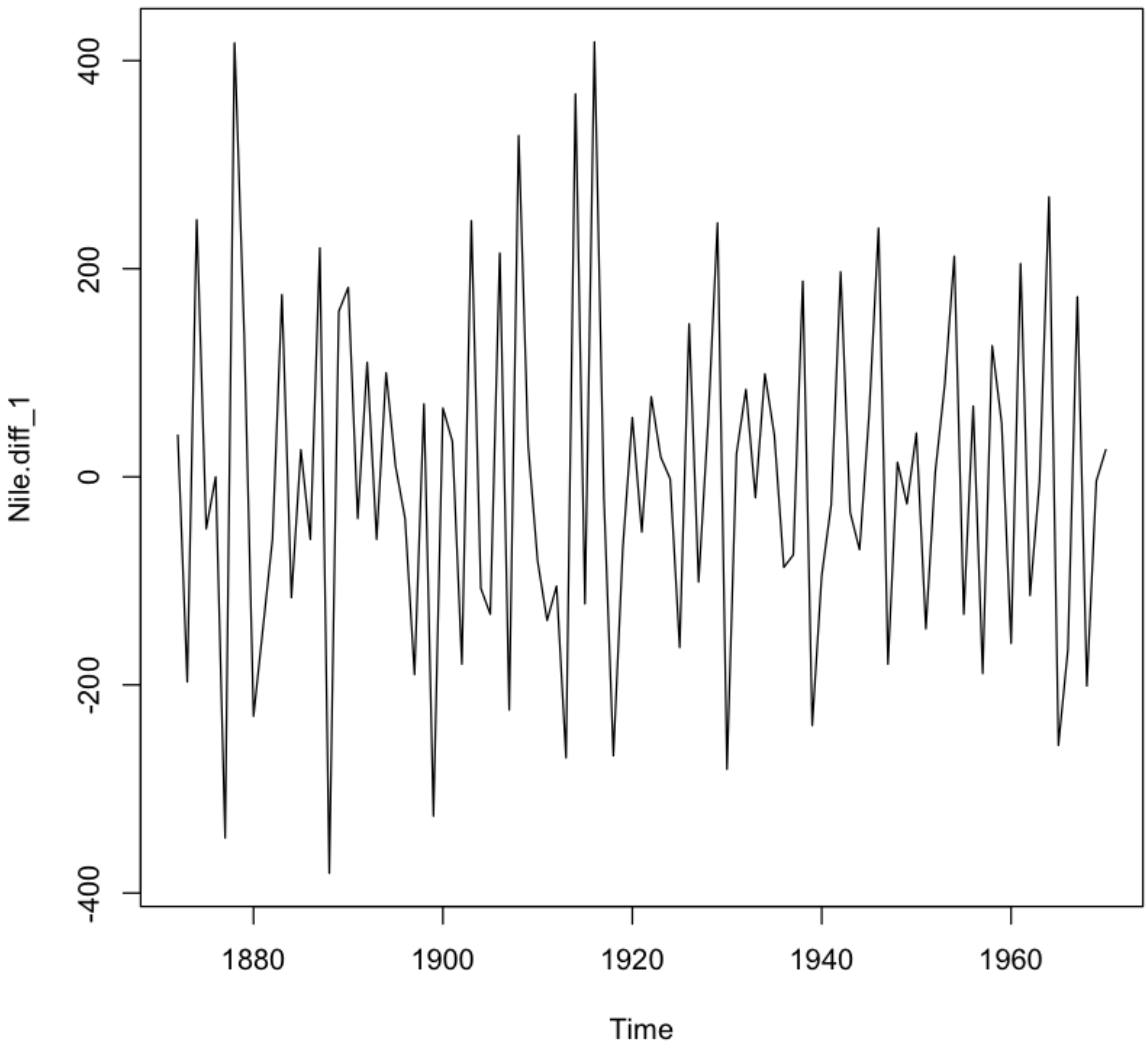
/images/posts/2022/1228/img_18.png

1번 차분을 한 결과 원 데이터보다는 평균이 일정해진 것처럼 보인다. 하지만 명확하지 않다. 한번 더 해보자.

2차 차분 진행

Nile.diff_2 <- diff(Nile, differences = 2)
plot(Nile.diff_2)

💻 출력결과

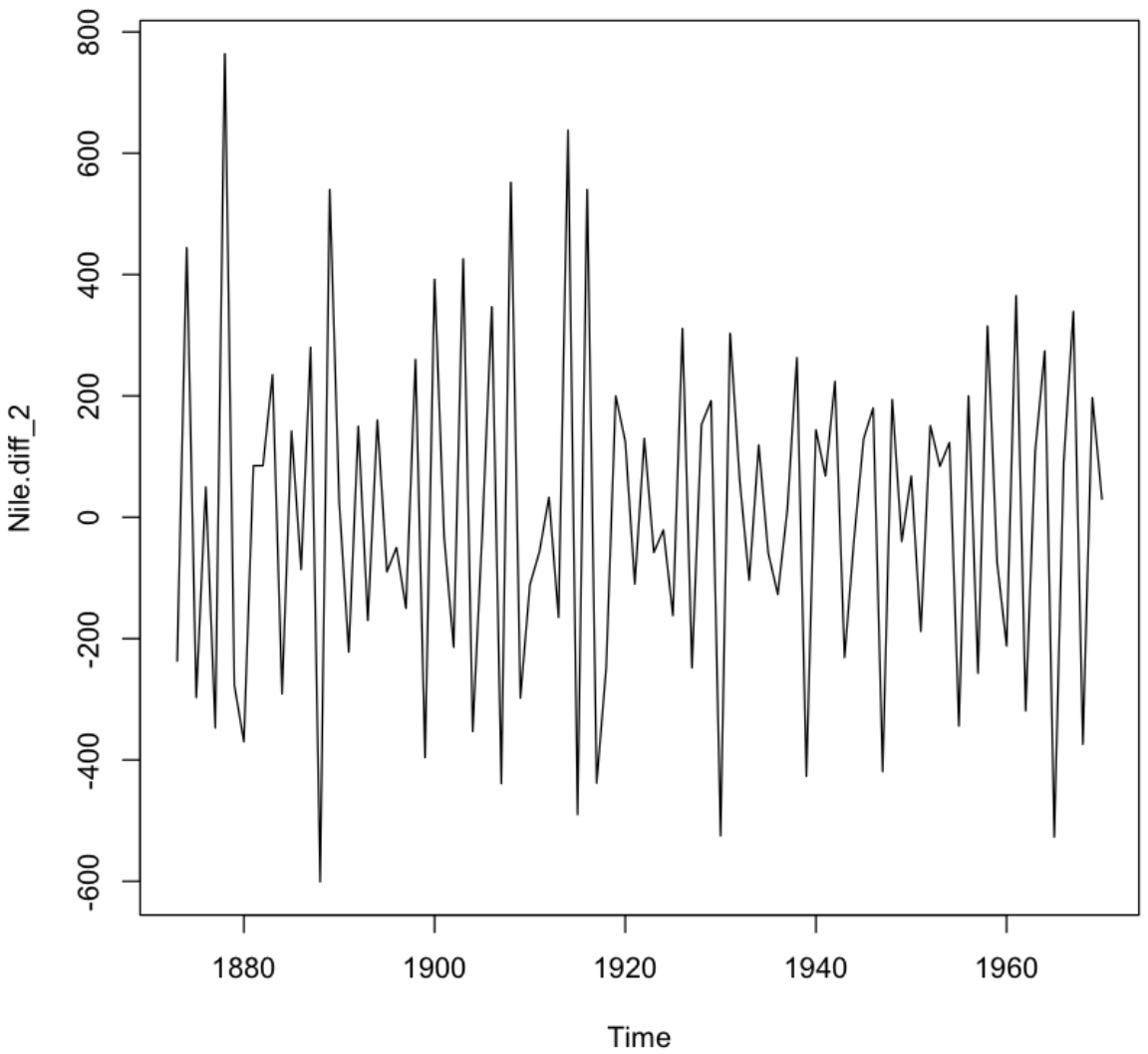
/images/posts/2022/1228/img_19.png

💡 차분을 2회 진행하니 1회 진행한 것보다도 평균과 분산이 시간이 지남에 따라서 일정한 정상성을 띄는 것을 확인할 수 있다. 이제 이 차분을 진행한 데이터 Nile.diff_2를 사용하여 자기상관함수와 부분자기상관함수를 통해서 AR/MA 모형의 여부를 살펴보자.

ACF와 PACF 를 통한 적합한 ARIMA 모델 결정

ACF 자기상관함수 그래프

acf(Nile.diff_2, lag.max=20)

💻 출력결과

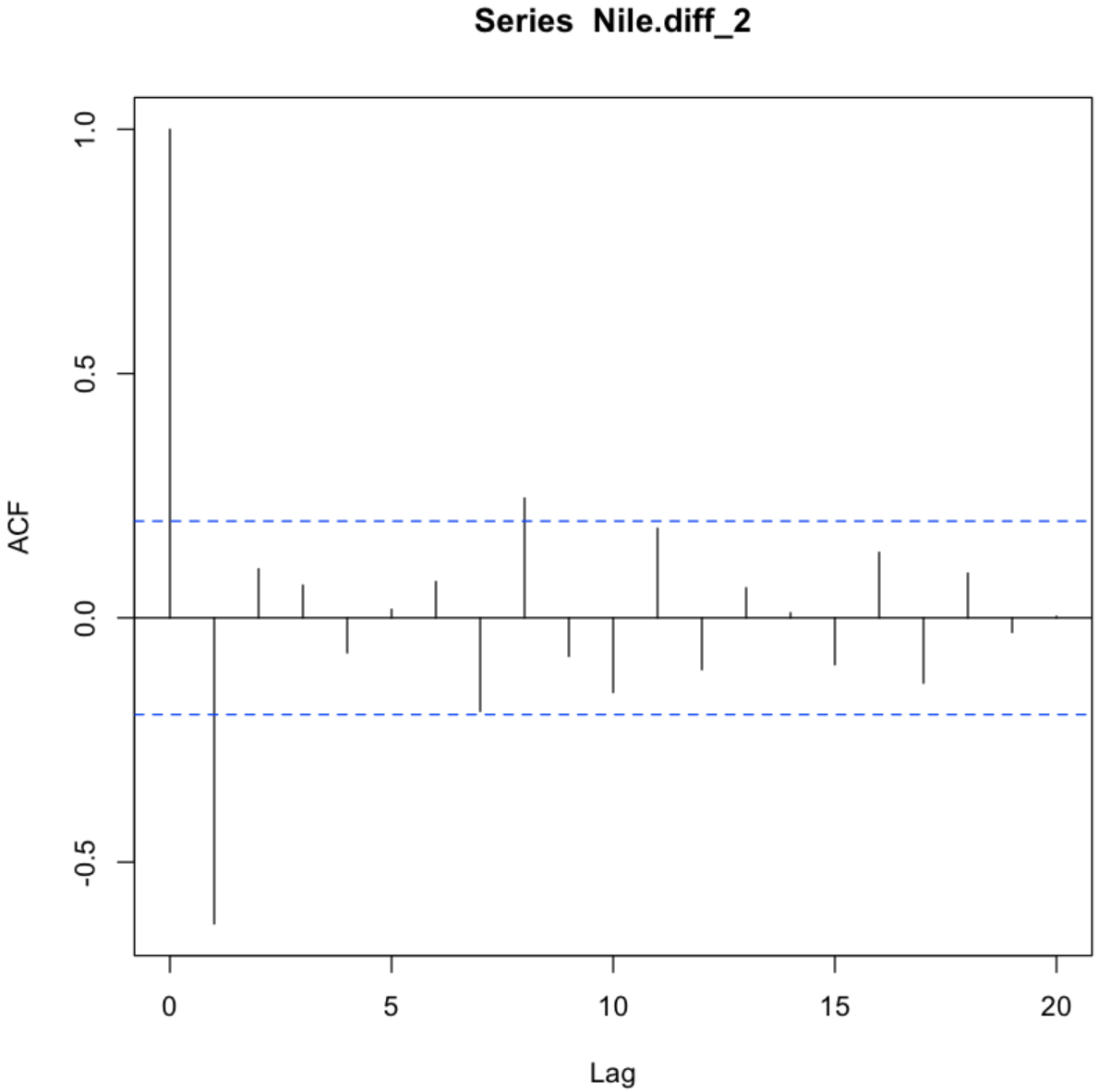
/images/posts/2022/1228/img_20.png

💡 1번째와 8번째 lag를 제외하고는 모두 신뢰구간안에 포함되어 있다.

ACF 자기상관함수 도표

acf(Nile.diff_2, lag.max=20, plot = FALSE)

💻 출력결과

/images/posts/2022/1228/img_21.png

PCAF 부분 자기 상관함수 그래프

pacf(king_ff1, lag.max=20)

💻 출력결과

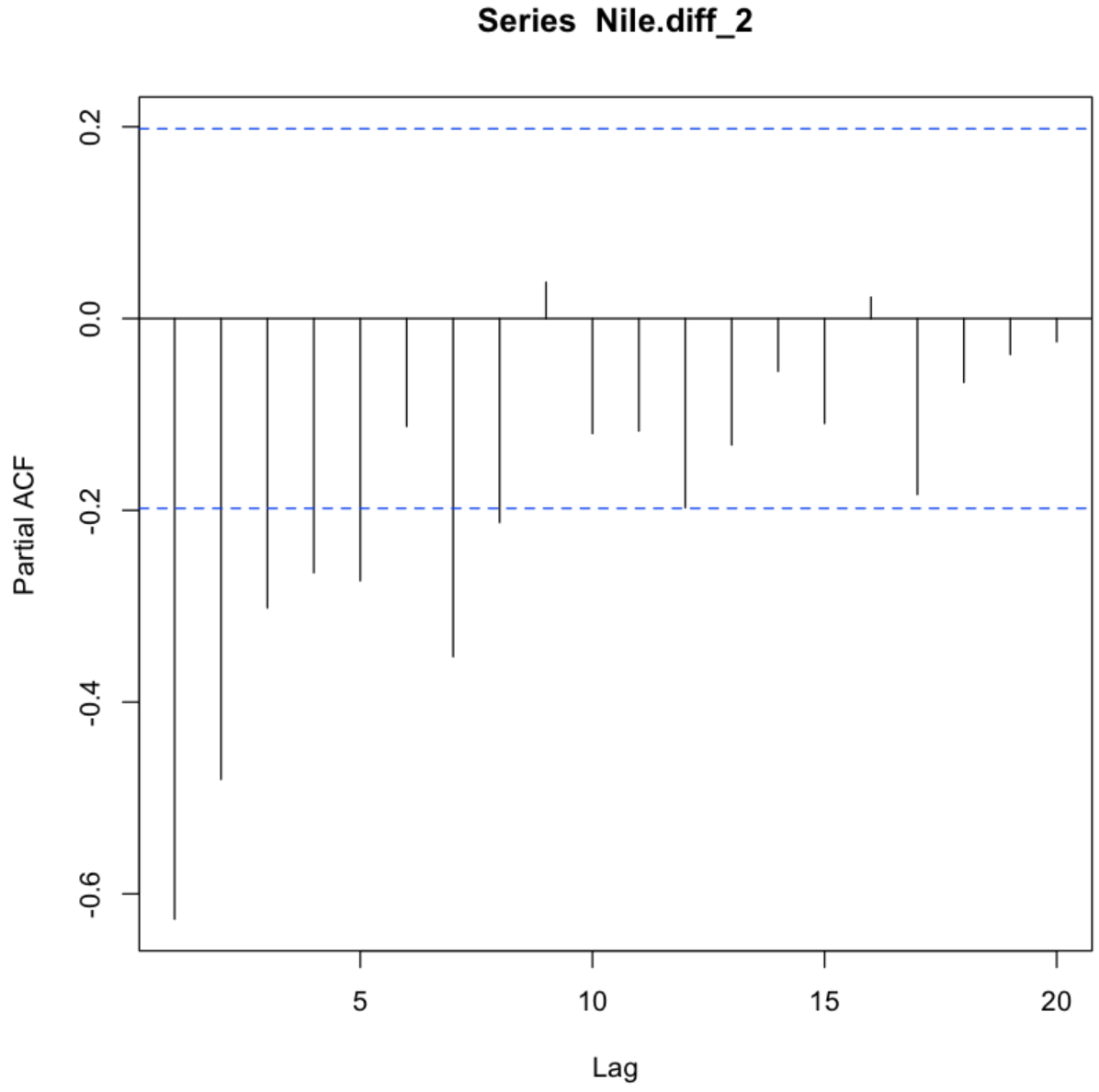
/images/posts/2022/1228/img_22.png

PCAF 부분 자기 상관함수 도표

pacf(king_ff1, lag.max=20, plot = FALSE)

💻 출력결과

/images/posts/2022/1228/img_23.png

4) 종합

부분자기상관함수는 pacf함수를 통해서 확인할 수 있다. 사용방법은 acf와 동일하다. 부분자기상관함수는 lag 1~8신뢰구간을 넘어 음의 값을 가지고 lag 9에서 절단이 된 것을 확인할 수 있다.

자기상관함수(ACF)와 부분자기상관함수(PACF)를 확인해 본 결과,

$ARMA(8,0)$ 부분자기상관함수 그래프를 볼 때, lag 9에서 절단
$ARMA(0,1)$ 자기상관함수 그래프에서 lag 2에서 절단

위의 결과처럼 단순 AR or MA로 모형을 나누기엔 결정하기가 좀 힘들다.

이처럼 어떤 모형을 선택해야할 지는 쉽지 않은 문제이다.

$ARMA(p,q)$에서는 AR모형과 MA 모형을 혼합하여 모형을 식별하고 결정할 필요가 있다. 만약 모수가 많다면 설명력은 커질 것이다. 하지만 모형이 복잡하고 이해하기는 더 어려워진다.

그렇다고 모수가 너무 적으면 모형이 단순해서 이해력은 높아지나 설명력이 낮아질 수 밖에 없다. 그렇기에 항상 Trade-Off는 존재한다.

5) 적절한 ARIMA 모형 찾기

forecast package 에 내장된 auto.arima() 함수 이용
ARMIA 모형 찾기

auto.arima(Nile)

💻 출력결과

Series: kings$age 
ARIMA(0,1,1) 

Coefficients:
          ma1
      -0.7218
s.e.   0.1208

sigma^2 estimated as 236.2:  log likelihood=-170.06
AIC=344.13   AICc=344.44   BIC=347.56

💡 적절한 ARIMA모형은 ARIMA(1, 1, 1)이다 .

6) 예측

arima 결과를 활용한 forecast 예측

#arima 결과 1,1,1 대입
Nile.arima <- arima(Nile, order=c(1,1,1))
#arima 결과를 활용한 forecast 예측
Nile.forecast <- forecast(Nile.arima, h = 10)
df <- data.frame(Nile.forecast)
df

💻 출력결과

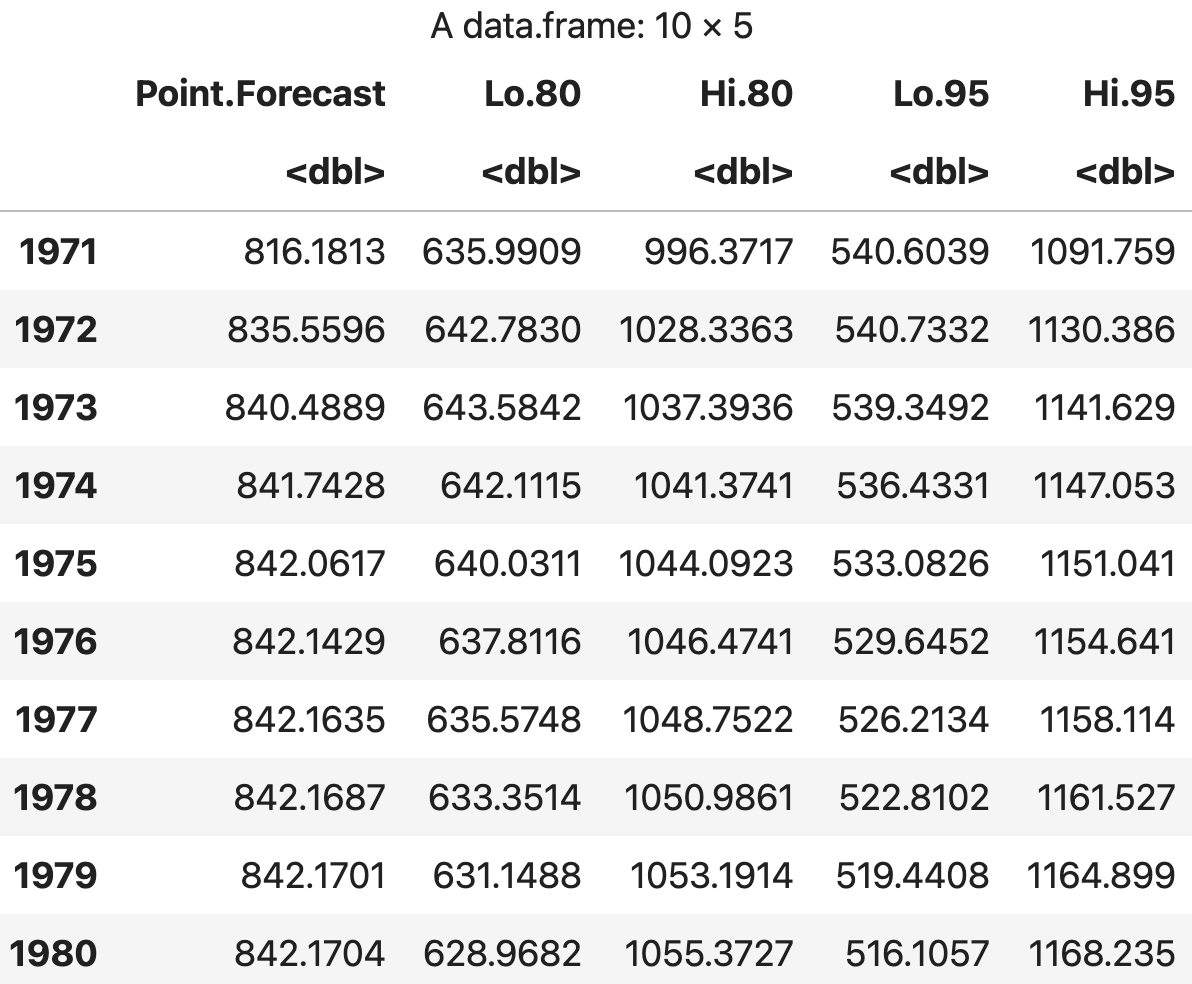
/images/posts/2022/1228/img_24.png

예측결과 시각화

예측 결과를 시각화 하기

plot(Nile.forecast)

💻 출력결과

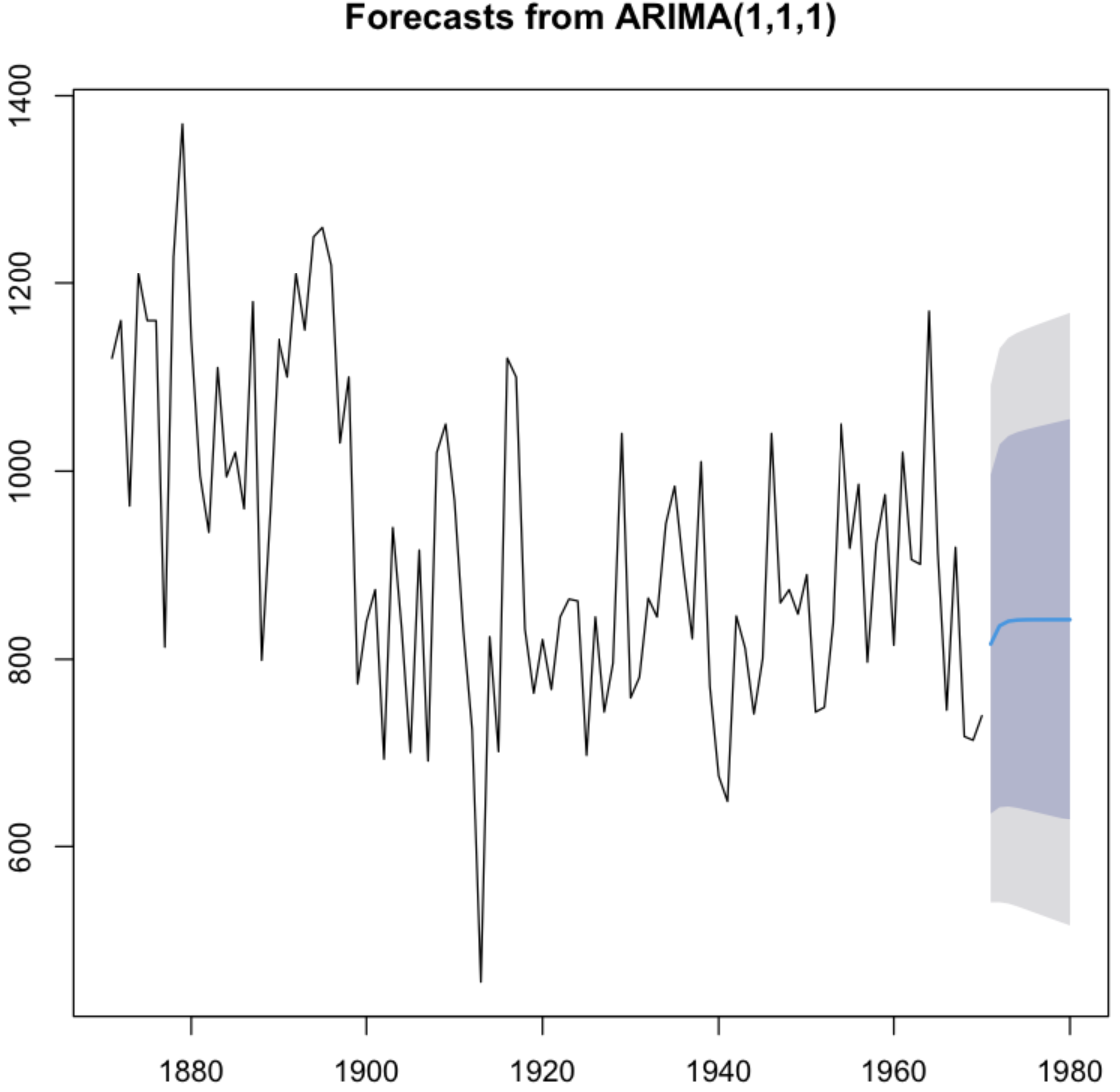
/images/posts/2022/1228/img_25.png

💡 진한 파란선이 점추정과 같은 회귀선이고 가장 높은 옅은 파란 영역(80%)과 회색영역(95%)이 신뢰구간인 구간예측값이다.