[R] 회귀분석

by 호쌤(이광호) on December 27, 2022

회귀분석의 사전적 의미는 ‘go back to an earlier and worse condition’(옛날의 대표적인 상태로 돌아감)입니다. 대표적인 상태를 토대로 미래의 어떤 결과를 예측하는 분석을 회귀분석이라고 합니다.

#01. 회귀분석(Regression analysis)의 이해

1) 회귀분석의 의미

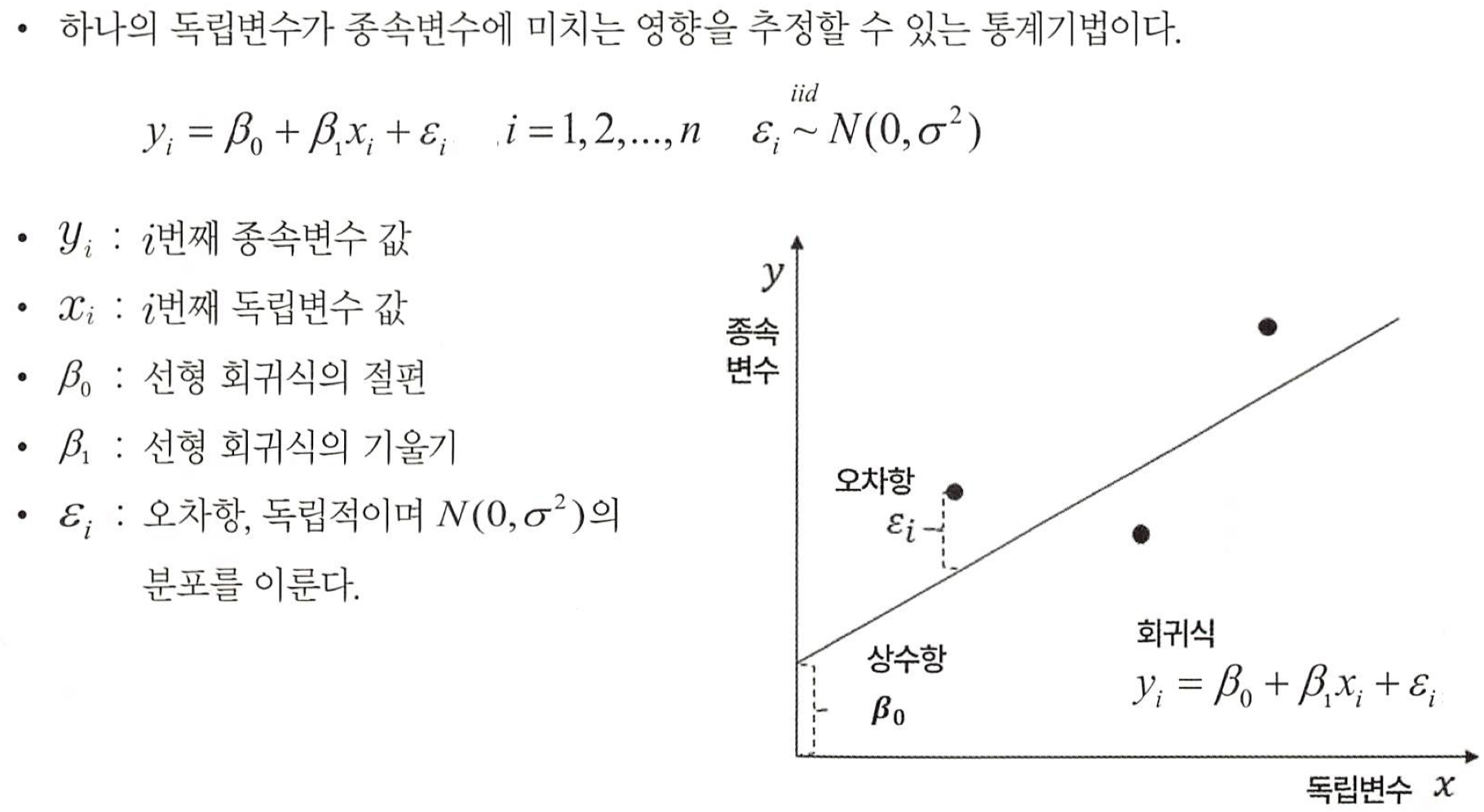
• 하나나 그 이상의 독립변수들이 종속변수에 미치는 영향을 추정할 수 있는 통계기법.
• 독립변수 X(설명변수)에 대하여 종속변수 Y(반응변수)들 사이의 관계를 수학적 모형을 이용하여 규명하는 것.

• 규명된 함수식을 이용하여 설명변수들의 변화로부터 종속변수의 변화를 예측하는 분석이다.
• 변수들 사이의 인과관계를 밝히고 모형을 적합하여 관심있는 변수를 예측하거나 추론하기 위한 분석방법이다 .
• 독립변수의 개수가 하나이면 단순선형회귀분석 , 독립변수의 개수가 두 개 이상이면 다중선형 회귀분석으로 분석할 수 있다 .

2) 회귀분석의 변수

영향을 받는 변수 ($y$)

반응변수 (response variable), 종속변수 (dependent variable), 결과변수(outcome variable)

영향을 주는 변수 ($x$)

설명변수 (explanatory variable), 독립변수 (independent variable), 예측변수 (predictor variable)

3) 회귀분석 예시

키(Height)에 따른 몸무게(Weight)

\[Y(weight) = a + b * X(height)\]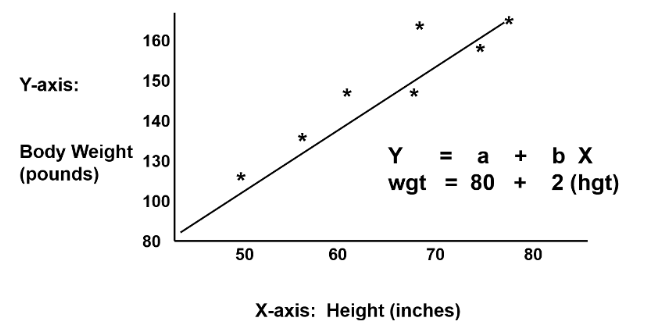

남자들의 평균 키

• 남자의 평균 Height는 175cm라 하자.
• 세대를 거듭할때마다, 높은 Height + 낮은 Height 사람들 혹은 보통 Height + 보통 Height 사람들이 다양하게 결혼하여 자녀를 낳을 것이다.
• 결국에는 남자들의 평균 Height는 175cm으로 회귀하려는 경향을 보일 것이다.

4) 선형회귀분석의 가정

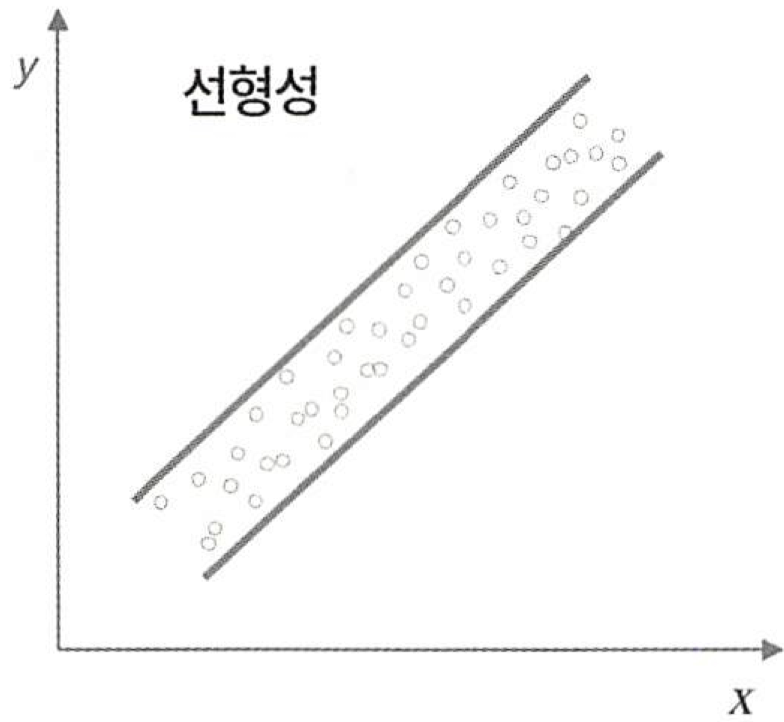
선형성

• 입력변수와 출력변수의 관계가 선형이다 .(선형회귀분석에서 가장 중요한 가정)
• 선형회귀모형에서는 왼쪽의 그래프와 같이 설명 변수(x)와 반응변수(y)가 선형적 관계에 있음이 전제 되어야 한다 .

등분산성

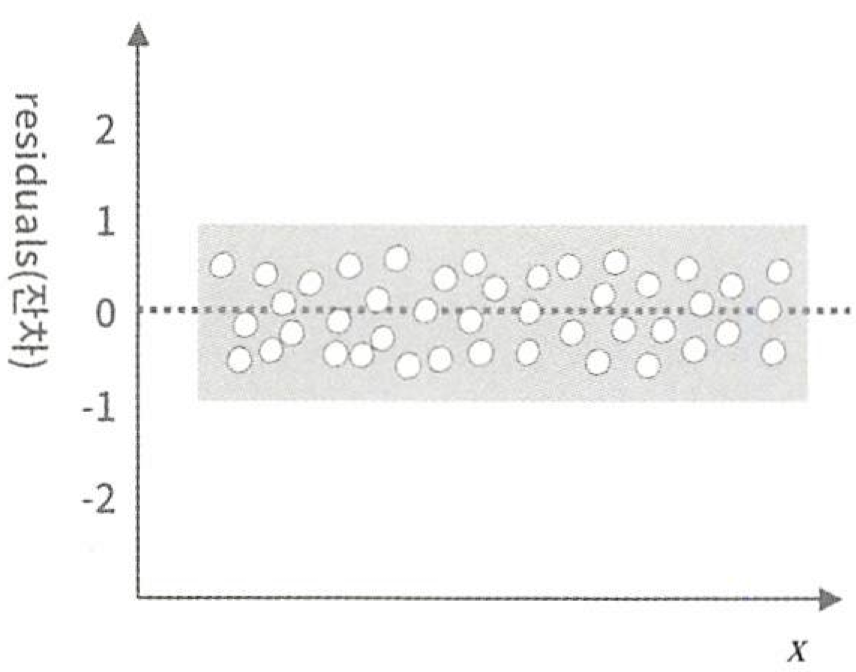
• 오차의 분산이 입력변수와 무관하게 일정하다 .
• 잔차플롯(산점도)를 활용하여 잔차와 입력 변수간에 아무런 관련성이 없게 무작위적으로 고루 분포되어야 등분산성 가정을 만족하게 된다 .
• 설명변수(X)에 대한 잔차의 산점도를 그렸을 때, 왼쪽의 그림과 같이 설명변수(X) 값에 관계없이 잔차들의 변동성 (분산)이 일정한 형태를 보이면 선형회귀분석의 가정 중 등분산성을 만족한다고 볼 수 있다 .

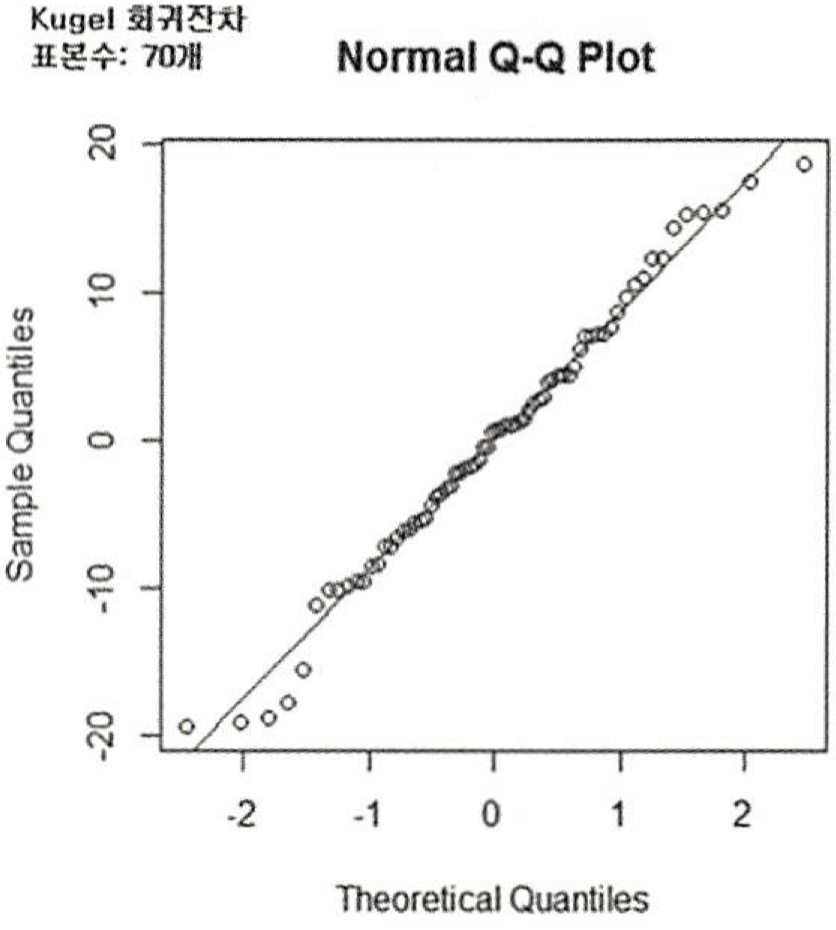
정상성 (정규성)

• Q-Q Plot을 출력했을 때, 왼쪽의 그림과 같이 잔차가 대각방향의 직선의 형태를 지니고 있으면 잔차는 정규분포를 따른다고 할 수 있다 .
• 오차의 분포가 정규분포를 따른다 . Q-Q plot, Kolmogolov-Smirnov 검정 , Shaprio-Wilk 검정 등을 활용하여 정규성을 확인한다 .

독립성

• 입력변수와 오차는 관련이 없다.
• 자기상관 (독립성)을 알아보기 위해 Durbin-Waston 통계 량을 사용하며 주로 시계열 데이터에서 많이 활용한다 .

비상관성

• 오차들끼리 상관이 없다.

5) 가정에 대한 검증

단순선형회귀분석

입력변수와 출력변수간의 선형성을 점검하기 위해 산점도를 확인한다 .

다중선형회귀분석

선형회귀분석의 가정인 선형성 등분산성，독립성 정상성이 모두 만족하는지 확인해야 한다 .

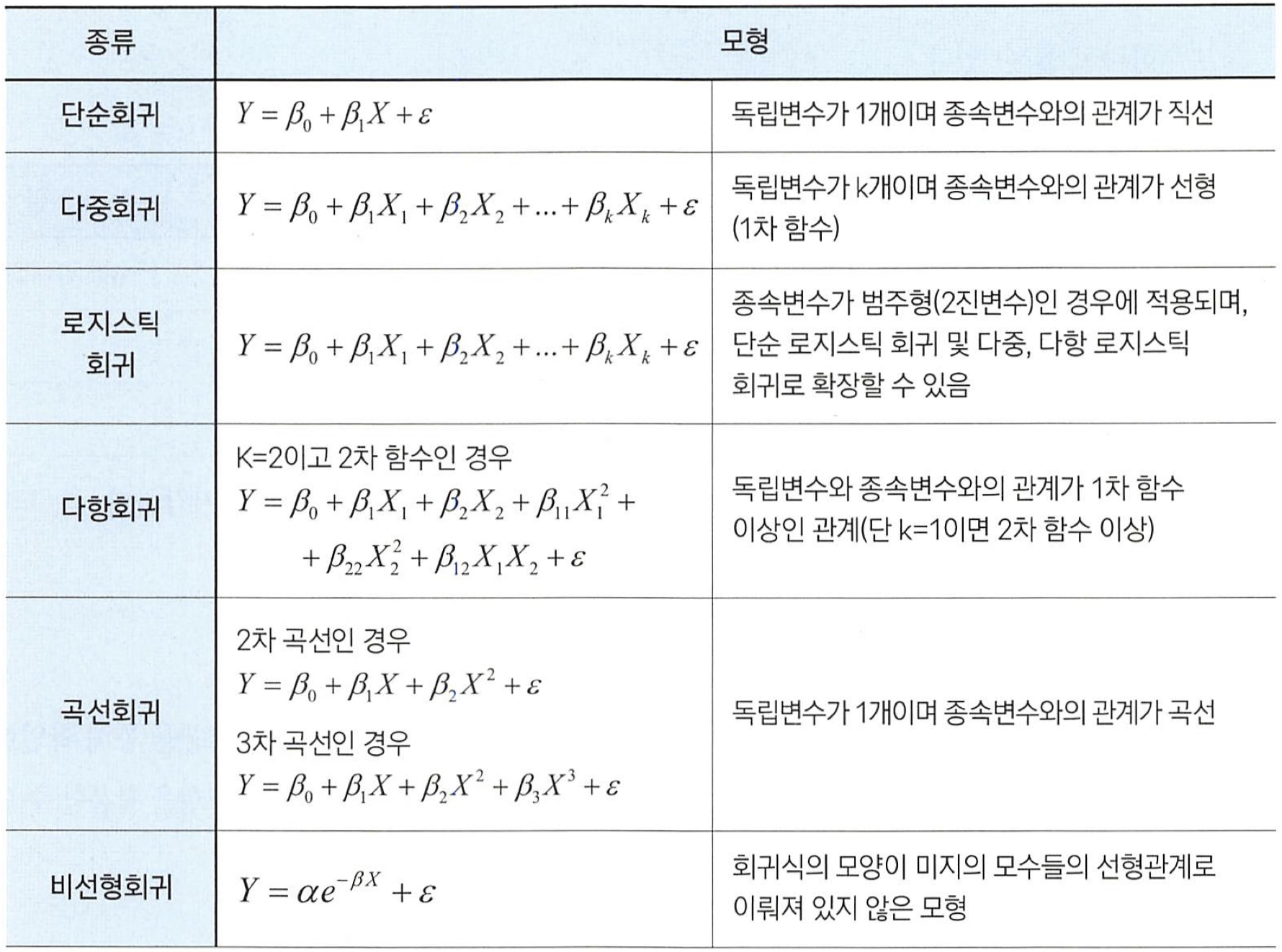
6) 회귀분석의 종류

#02. 회귀분석 통계 검정

1) 예측변수(회귀계수)들이 유의미한가 ?

• 각 독립변수($x$)의 회귀계수($b$)가 유의한가?
• t-검정을 사용
• 해당 계수의 t 통계량의 p-값이 0.05 보다 작으면 해당 회귀계수가 통계적으로 유의하다고 볼 수 있다.

2) 모형이 얼마나 설명력을 갖는가 ?

• 만들어진 회귀모형(예측모형)이 유의한가?
• 주어진 모든 변수들이 함께 어느 정도 예측변수의 변량을 설명(예측)하는가?
• 결정계수 ($R^2$)를 확인한다 . 결정계수는 0~1 값을 가지며，높은 값을 가질수록 추정된 회귀식의 설명력이 높다 .

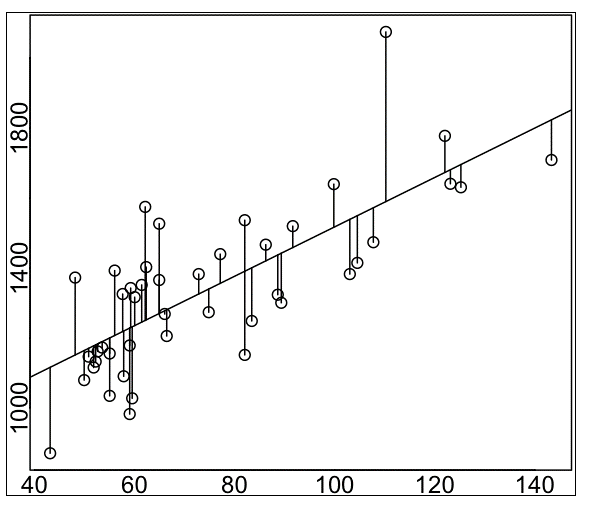
3) 모형이 데이터를 잘 적합하고 있는가 ?

• 잔차를 그래프로 그리고 회귀진단을 한다 .

#03. cars 데이터를 활용한 회귀분석

1) 데이터 확인하기

1920년대에 조사된 데이터로, 차량이 달리는 속도와 그 속도에서 브레이크를 잡았을 때 제동거리를 측정한 데이터.

R에 기본적으로 내장되어 있다.

head(cars)

💻 출력결과

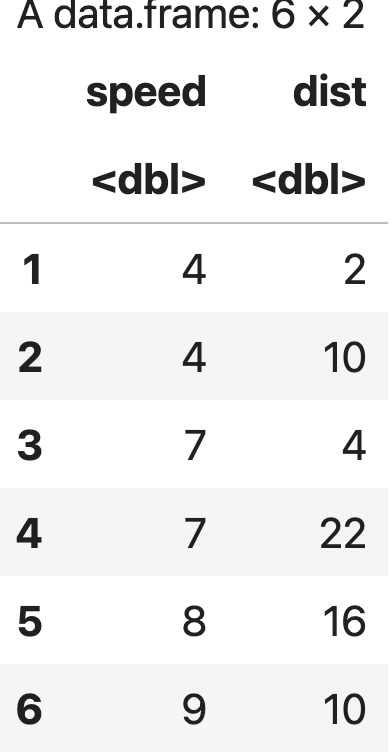
2) 데이터 분포 조사

히스토그램을 통해 데이터 분포를 조사한다.

# 화면을 1행 2열로 분할함
par(mfrow=c(1,2))
# 속도에 대한 히스토그램
hist(cars$speed)
# 제동거리에 대한 히스토그램
hist(cars$dist)
# 화면을 다시 1행 1열로 원복함
par(mfrow=c(1,1))

💻 출력결과

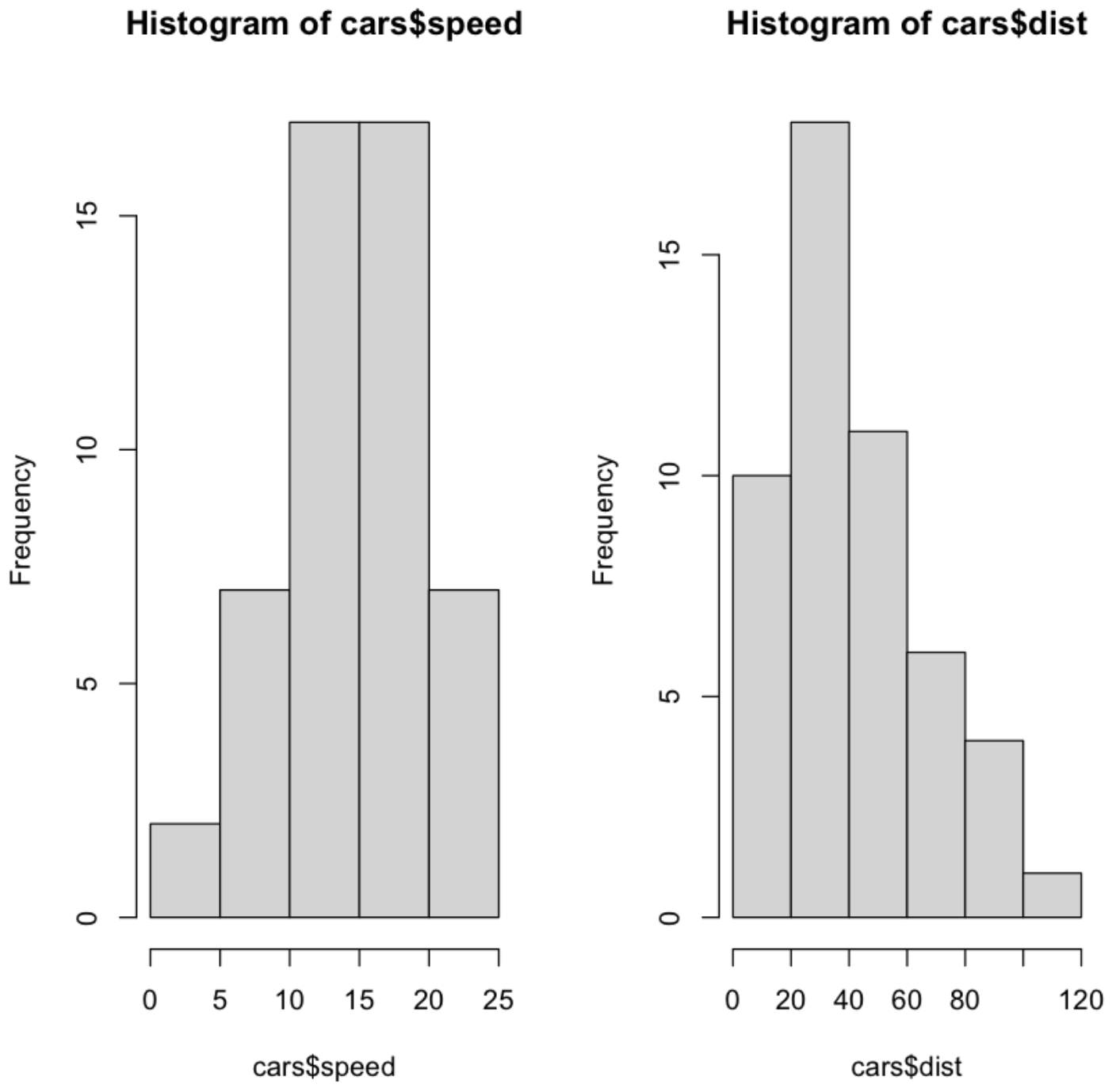
산점도 그래프를 통한 데이터 분포 조사

plot(dist~speed,data=cars)

💻 출력결과

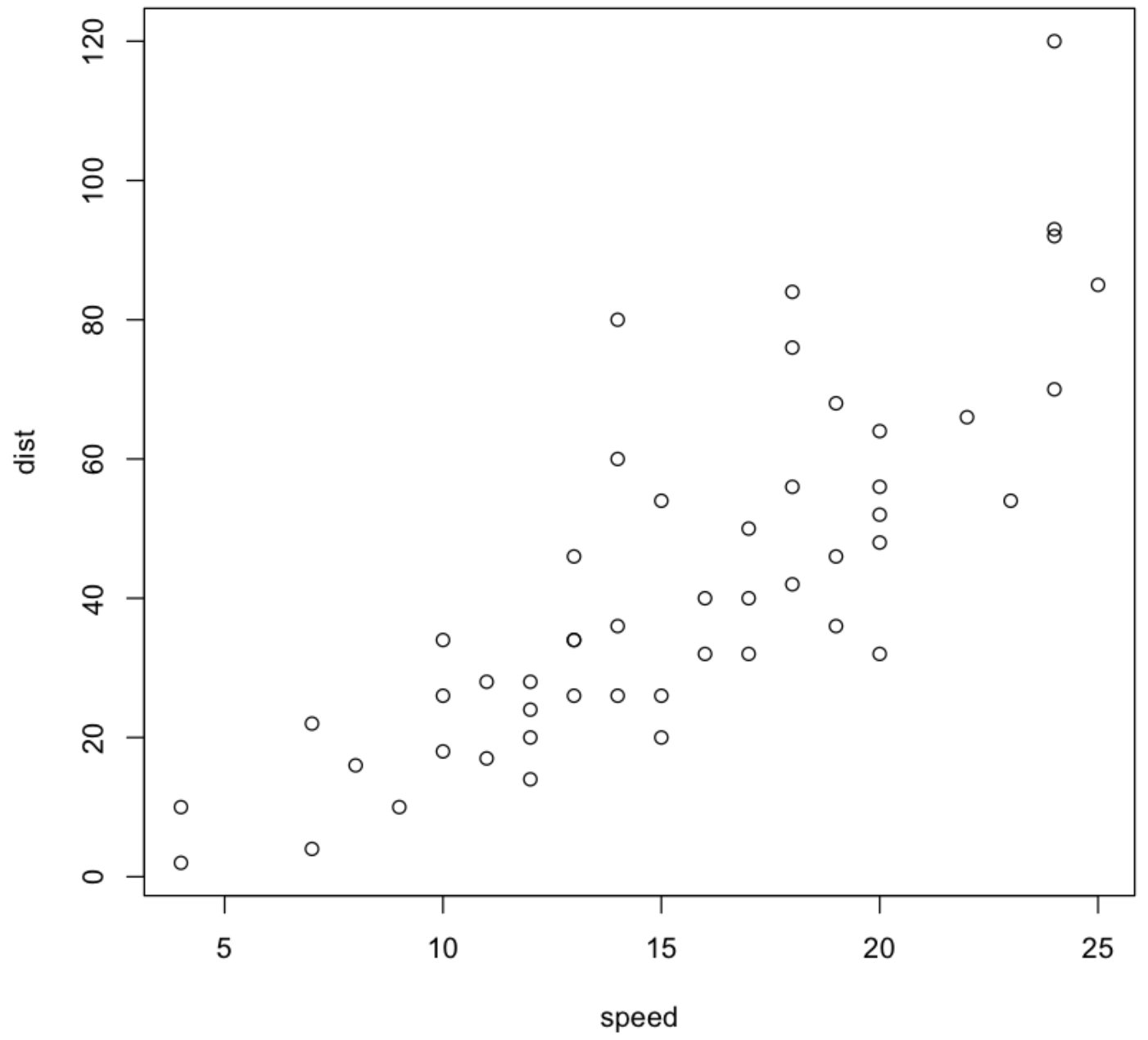
3) 속도에 따른 제동거리에 대한 회귀분석

R에서 회귀분석은 lm() 함수를 사용하고, 결과는 lm() 함수로부터 리턴받은 객체를 summary() 함수에 전달하여 확인할 수 있다.

model = lm(dist ~ speed, data = cars)
summary(model)

💻 출력결과

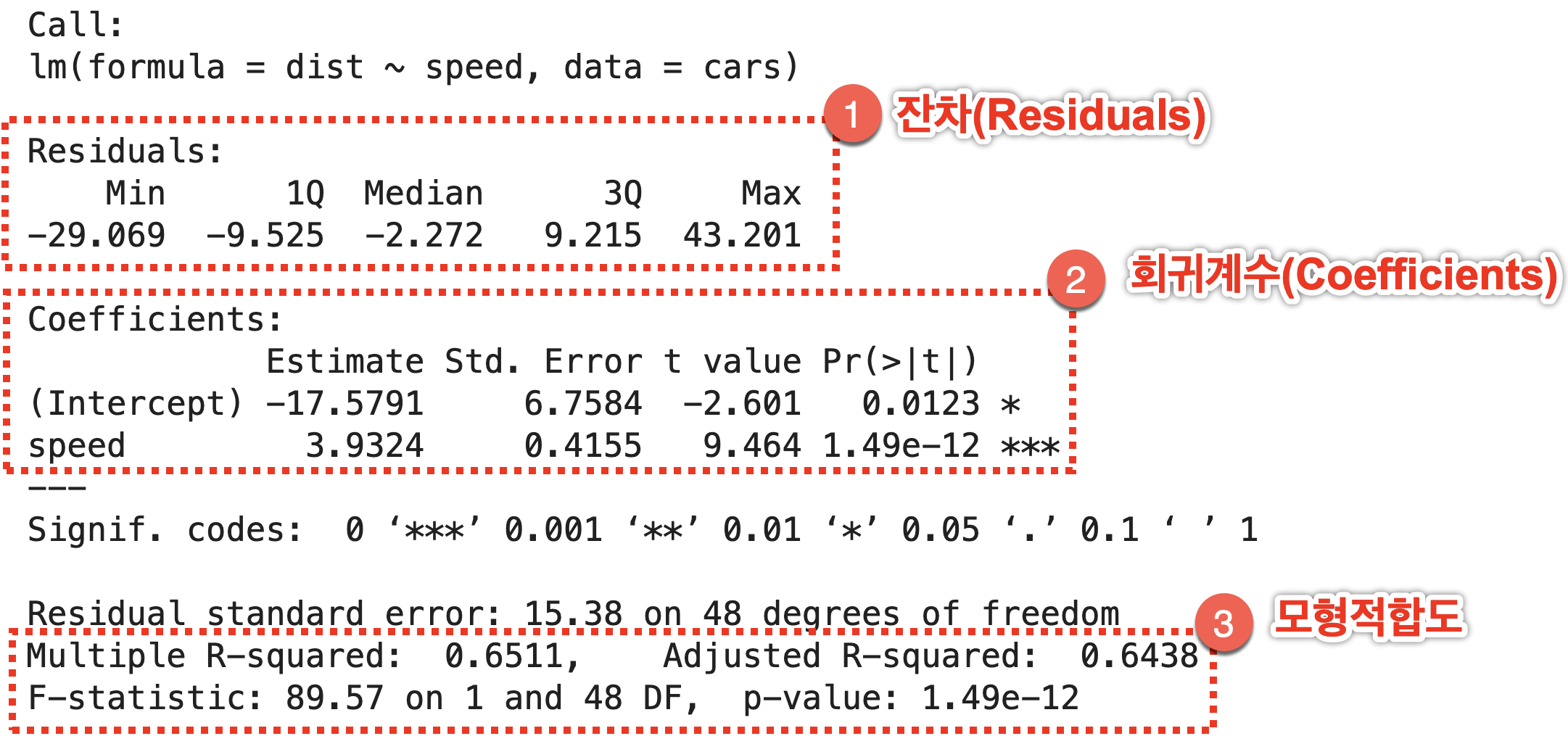
4) 회귀분석결과 해석하기

잔차(Residuals)

Residuals:
    Min      1Q  Median      3Q     Max
-29.069  -9.525  -2.272   9.215  43.201

• 잔차는 예측값과 실제값의 차이를 나타낸다.
• 잔차의 최솟값(Min), 사분위수(1Q, Median, 3Q), 최댓값(Max)을 보여준다.
• 중앙값(median)이 0에 가깝고, 1사분위 점수(Q1)와 3사분위 점수(Q3)가 거의 대칭을 이루고 있으므로, 잔차가 정규분포에서 거의 벗어나지 않았다고 볼 수 있다.

회귀계수(Coefficients)

Coefficients:
            Estimate                    Pr(>|t|)    
(Intercept) -17.5791                      0.0123    
speed         3.9324                    1.49e-12

• Estimate는 데이터로부터 얻은 계수의 추정치(estimate)를 말한다.
• 절편(Intercept)의 추정치는 -17.5791로, speed가 0일 때 dist의 값이다.
• speed의 계수 추정치는 3.9324로 speed가 1 증가할 때마다 dist가 3.9324 증가한다는 것을 의미한다.
• 추정치의 오른쪽 끝의 Pr(>|t|)는 모집단에서 계수가 0일 때, 현재와 같은 크기의 표본에서 이러한 계수가 추정될 확률인 p값을 나타낸다.
• 이 확률이 매우 작다는 것은, 모집단에서 speed의 계수가 정확히 3.9324는 아니더라도 현재의 표본과 비슷하게 0보다 큰 어떤 범위에 있을 가능성이 높다는 것을 의미한다.
• 보통 5%와 같은 유의수준을 정하여 p값이 그보다 작으면(p < 0.05), “통계적으로 유의하다”라고 한다.
• 즉, speed가 증가할 때 기대되는 dist의 변화는 유의수준 5%에서 통계적으로 유의미하다.

회귀식

\[dist = -17.5791 + 3.9324 × speed\]

모형적합도

Multiple R-squared:  0.6511,    Adjusted R-squared:  0.6438
F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

Multiple R-squared, Adjusted R-squared, F-statistic, p-value는 모형이 데이터에 잘 맞는 정도를 보여주는 지표들이다.

Multiple R-squared: 0.6511

• 모형 적합도(혹은 설명력)
• dist의 분산을 speed가 약 65%를 설명한다
• 각 사례마다 dist에 차이가 있다.

Adjusted R-squared: 0.6438

• 독립변수가 여러 개인 다중회귀분석에서 사용
• 독립변수의 개수와 표본의 크기를 고려하여 R-squared를 보정
• 서로 다른 모형을 비교할 때는 이 지표가 높은 쪽은 선택한다

F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12

• 회귀모형에 대한 (통계적) 유의미성 검증 결과, 유의미함 (p < 0.05)
• 즉, 이 모형은 주어진 표본 뿐 아니라 모집단에서도 의미있는 모형이라 할 수 있음

5) 결과보고

논문 등에서 회귀분석의 결과는 다음 순서대로 보고한다.

모형적합도 보고

F분포(연속확률분포)의 파라미터 2개와 그 때의 F값, p-value와 유의수준의 비교를 적시한다.

dist에 대하여 speed로 예측하는 회귀분석을 실시한 결과, 이 회귀모형은 통계적으로 유의미하였다. (F(1,48) = 89.57, p < 0.05).

독립변수 보고

speed의 회귀계수는 3.9324로, dist에 대하여 유의미한 예측변인인 것으로 나타났다 (t(48) = 9.464, p < 0.05).

#04. Galton 데이터를 예제로 회귀분석

1) 데이터 확인하기

galton 데이터는 UsingR 패키지에 포함된 샘플로 928개의 부모의 평균키와 아이의 키에 대한 자료이다.

패키지 설치하기

REPO_URL <- "https://cran.seoul.go.kr/"

if (!require("UsingR")) {
    install.packages("UsingR", repos=REPO_URL)
}
library(UsingR)

데이터 확인하기

head(galton)

💻 출력결과

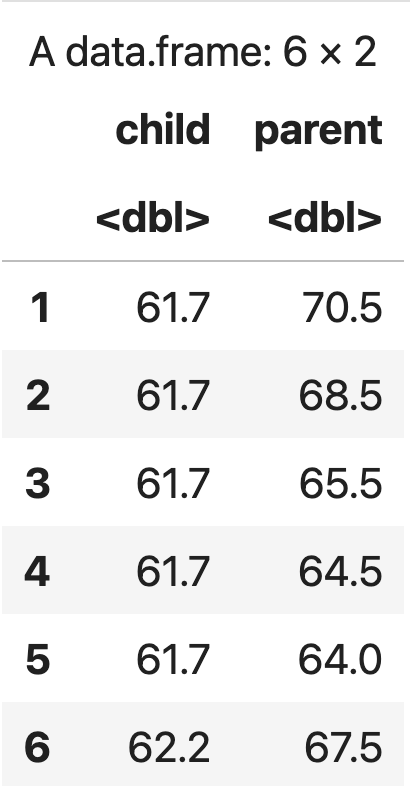
2) 데이터 분포 조사

히스토그램을 통해 데이터 분포를 조사한다.

par(mfrow=c(1,2))
hist(galton$child)
hist(galton$preant)
par(mfrow=c(1,1))

💻 출력결과

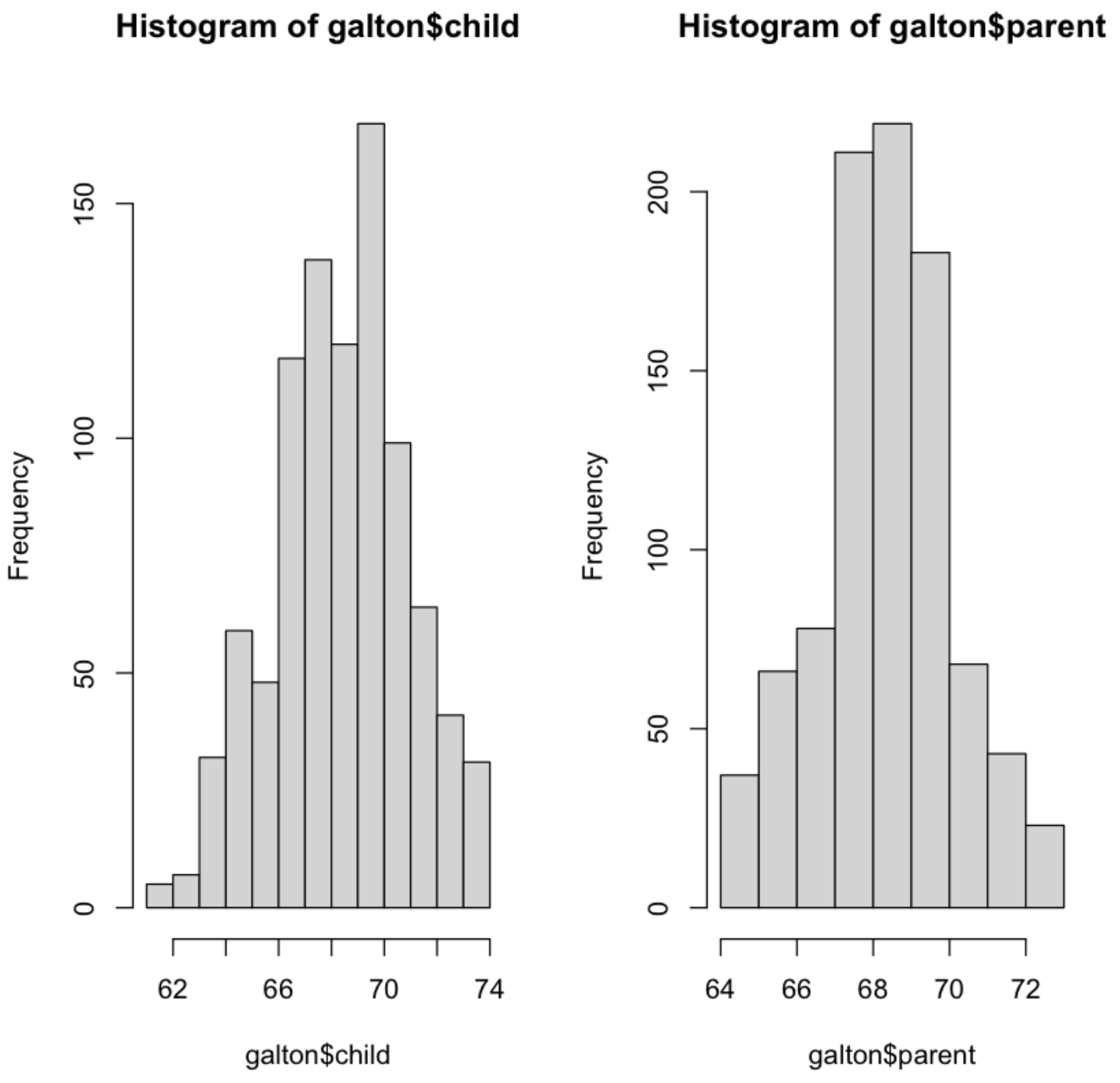
산점도 그래프를 통한 데이터 분포 조사

plot(child~parent,data=galton)

💻 출력결과

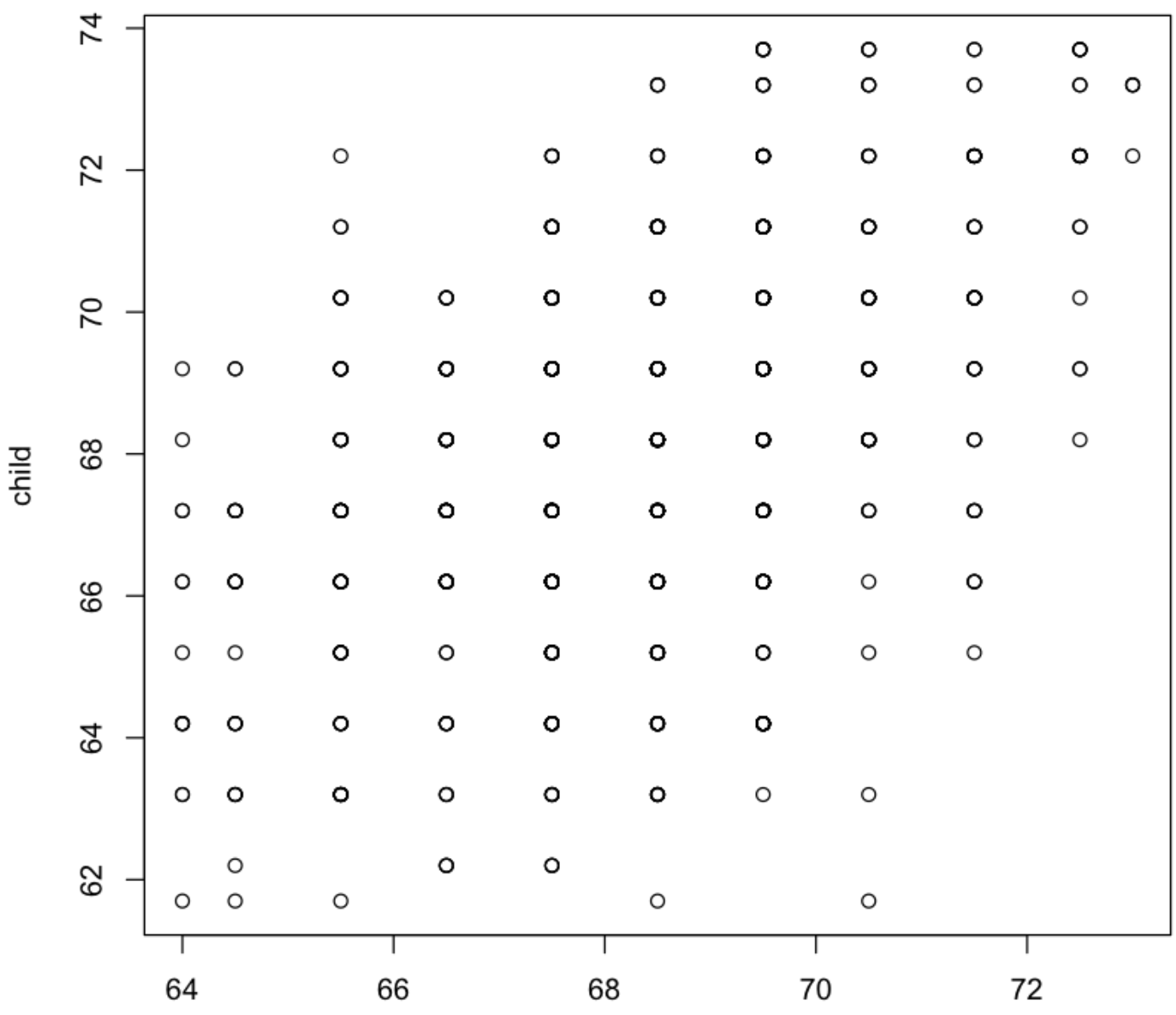
3) 부모키에 따른 자식 키에 대한 회귀분석

R에서 회귀분석은 lm() 함수를 사용하고, 결과는 lm() 함수로부터 리턴받은 객체를 summary() 함수에 전달하여 확인할 수 있다.

lm_model <- lm(child~parent, data=galton)
summary(lm_model)

💻 출력결과

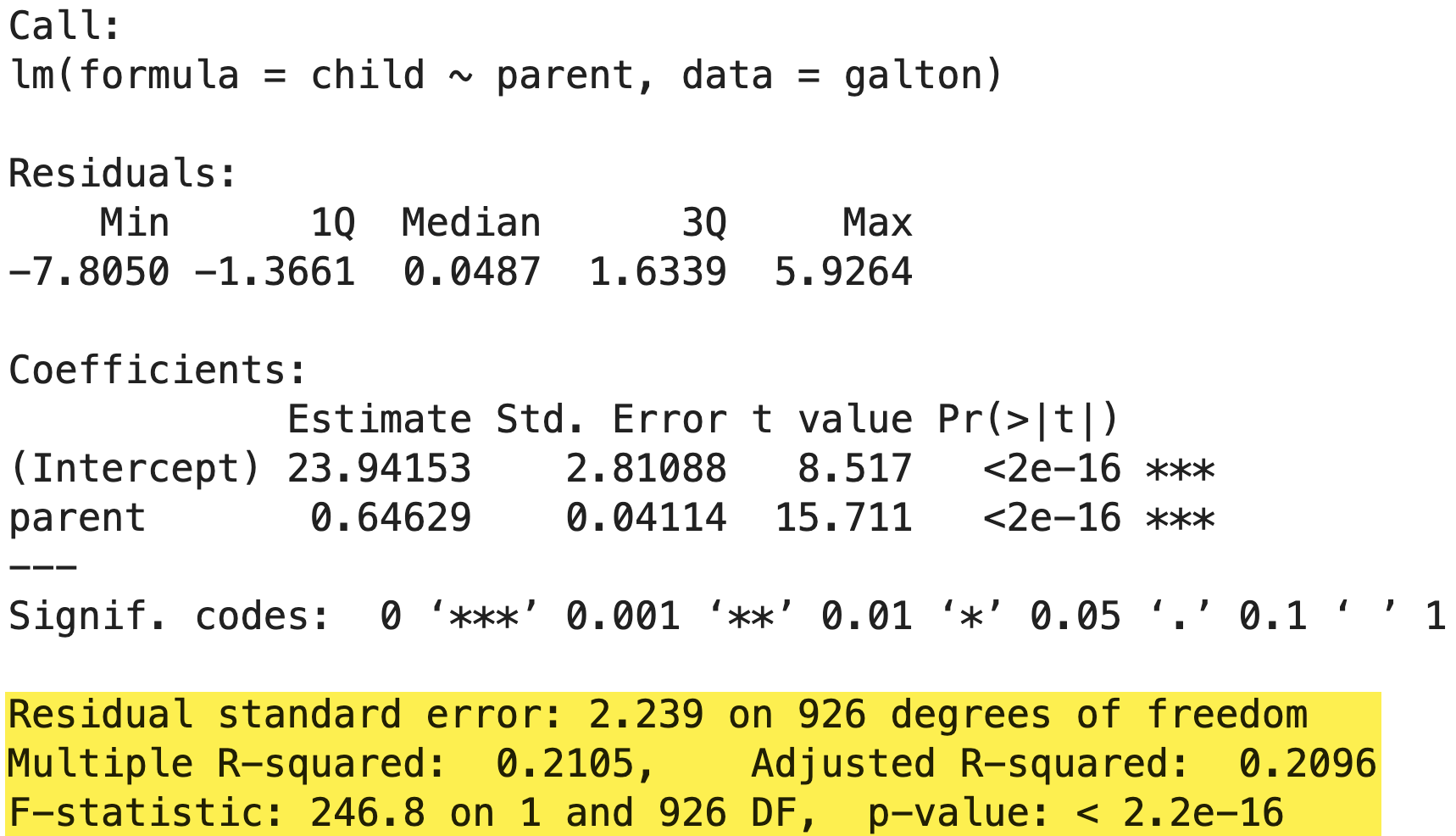
4) 회귀분석결과 해석하기

잔차

중앙값(median)이 0에 가깝고(0.0487), 1사분위 점수(Q1)와 3사분위 점수(Q3)가 거의 대칭을 이루고 있으므로, 잔차가 정규분포에서 거의 벗어나지 않았다고 볼 수 있다.

회귀계수

• 절편(Intercept)의 추정치: 23.94153
• p-value가 $2.2e-16$ 로 나타나 유의 수준은 0.05보다 작으므로 회귀계수의 추정치들이 “통계적으로 유의하다”

결정계수

• 결정계수(0~1사이)는 0.2105 로 다소 낮게 이 모형은 자녀키 분산의 21.0%를 설명해준다는 뜻이다.

회귀식

• parent의 계수 추정치: 0.64629로 parent가 1 증가할 때마다 child가 0.64629증가.

\[child = 23.94153 + 0.64629 \times parent\]

분석결과를 그래프로 표현하기

plot(child~parent,data=galton)
abline(lm_model,col="red")

💻 출력결과

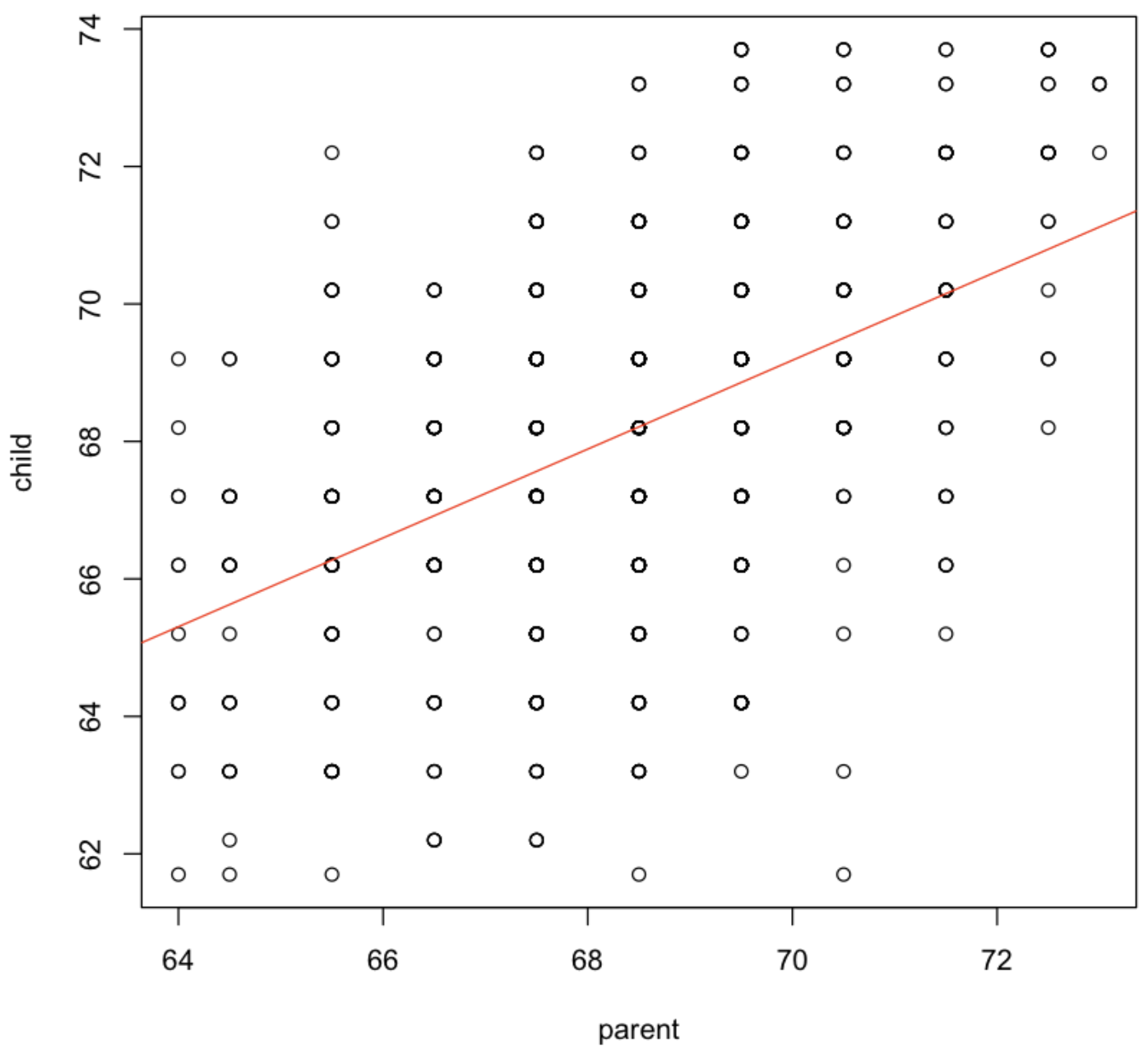
5) 결과보고

모형적합도 보고

자식의 키child에 대하여 부모의 평균키 parent로 예측하는 회귀분석을 실시한 결과, 이 회귀모형은 통계적으로 유의미하였다. (F(1,926) = 246.8, p < 0.05).

독립변수 보고

parent의 회귀계수는 0.64629로, child에 대하여 유의미한 예측변인인 것으로 나타났다 (t(926) = 15.717, p < 0.05).

#05. 10년간 에어컨 예약대수에 따른 판매대수 회귀분석

1) 데이터 확인하기

에어컨의 예약대수 $x$와 판매대수 $y$에 대한 가상의 데이터를 정의한다.

데이터 정의하기

# 10년간 에어컨 예약대수
x <- c(19, 23, 26, 29, 30, 38, 39, 46, 49)
# 10년간 에어컨 판매대수
y <- c(33, 51, 40, 49, 50, 69, 70, 64, 89)
# 데이터프레임으로 병합
aircon = data.frame(x, y)
aircon

💻 출력결과

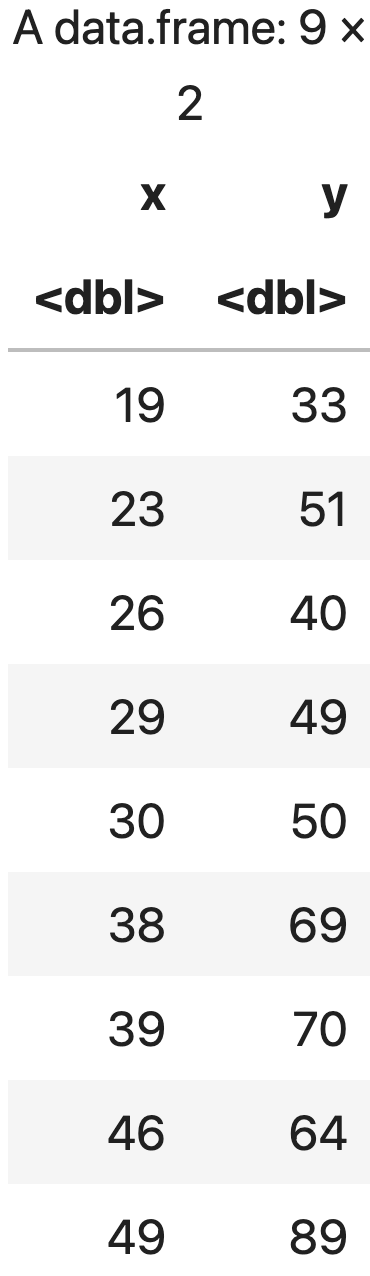
2) 데이터 분포 조사

히스토그램을 통한 분포 조사

par(mfrow=c(1,2))
hist(aircon$x)
hist(aircon$y)
par(mfrow=c(1,1))

💻 출력결과

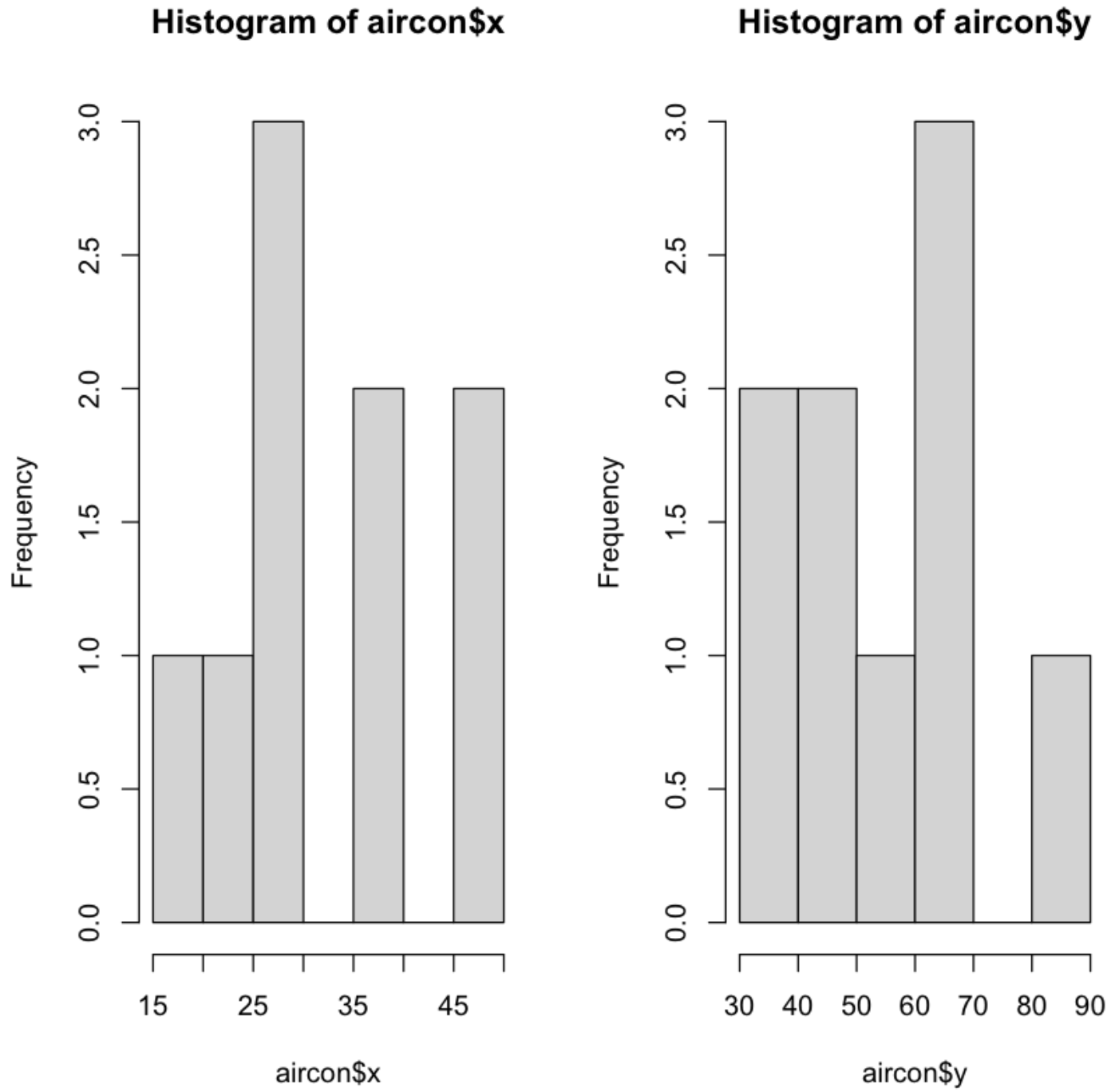
Q-Q Plot을 통한 데이터 분포 조사

plot(y~x,data=aircon)

💻 출력결과

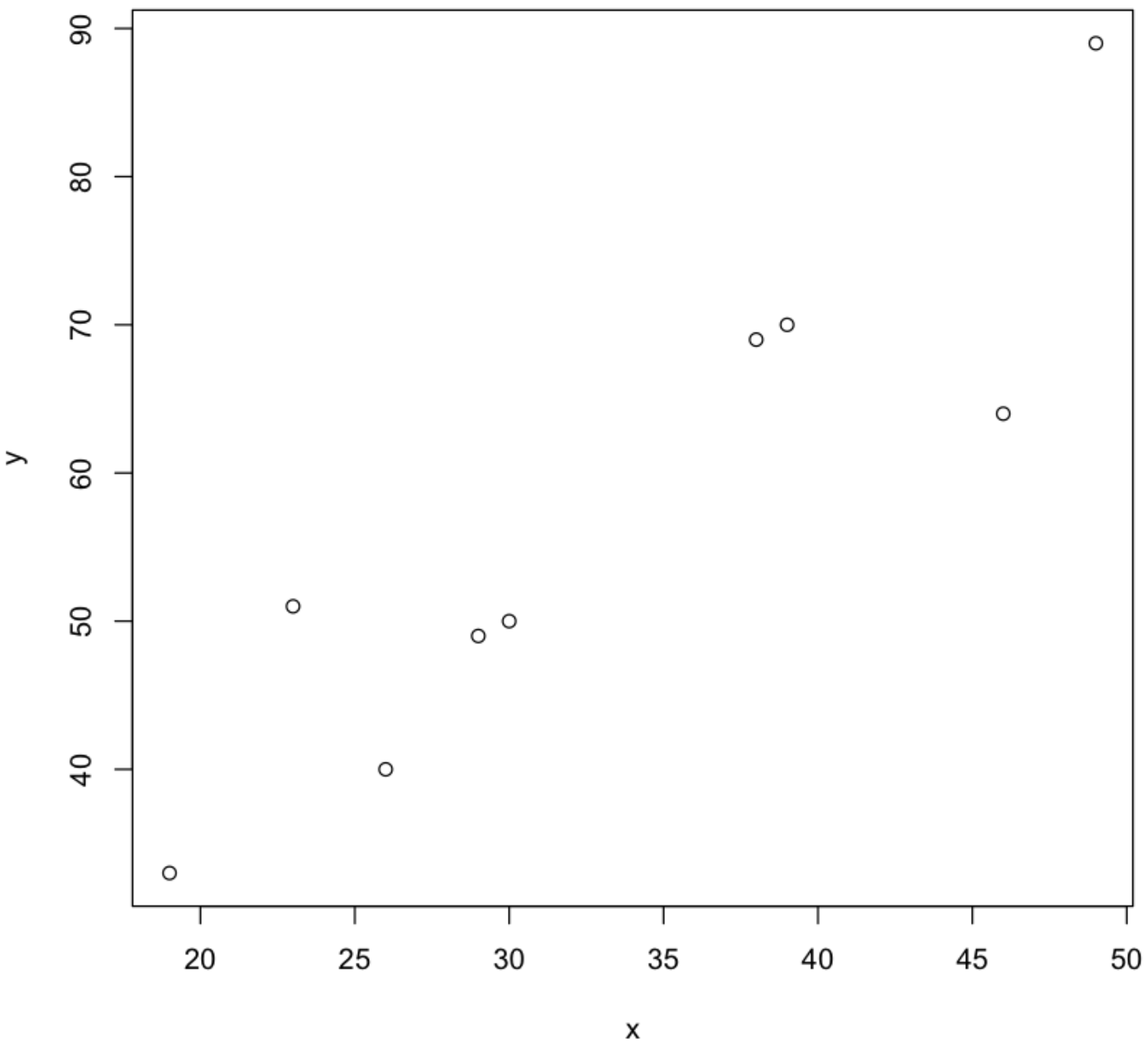
3) 에어컨 예약 대수에 따른 판매 대수를 예측하기 위한 회귀분석

model = lm(y ~ x, data = aircon)
summary(model)

💻 출력결과

Call:
lm(formula = y ~ x, data = aircon)

Residuals:
    Min      1Q  Median      3Q     Max 
-12.766  -2.470  -1.764   4.470   9.412 
        
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   6.4095     8.9272   0.718 0.496033    
x             1.5295     0.2578   5.932 0.000581 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.542 on 7 degrees of freedom
Multiple R-squared:  0.8341,	Adjusted R-squared:  0.8104 
F-statistic: 35.19 on 1 and 7 DF,  p-value: 0.0005805

4) 결과해석

잔차

중앙값(median)이 0에 가깝고(-1.764), 1사분위 점수(Q1)와 3사분위 점수(Q3)가 거의 대칭을 이루고 있으므로, 잔차가 정규분포에서 거의 벗어나지 않았다고 볼 수 있다.

회귀계수

• 절편(Intercept)의 추정치: 6.4095
• p-value가 0.0005805 로 나타나 유의 수준은 0.05보다 작으므로 회귀계수의 추정치들이 “통계적으로 유의하다”

결정계수

• 결정계수(0~1사이)는 0.8341 으로 높게 나타나 이 회귀식이 데이터를 적절하게 설명하고 있다고는 할 수 있다 .
• 결정계수가 높아 데이터의 설명력이 높고 회귀분석결과에서 회귀식과 회귀계수들이 통계적으로 유의하므로 에어컨 판매대수를 에어컨 에약대수로 추정할 수 있다 .

회귀식

• x의 계수 추정치: 1.5295로 x가 1 증가할 때마다 y가 1.5295증가.

\[y = 1.5295 \times x + 6.4095\]

5) 결과보고

모형적합도 보고

에어컨 예약대수x에 대한 판매대수y를 예측하는 회귀분석을 실시한 결과, 이 회귀모형은 통계적으로 유의하였다. (F(1,7) = 35.19, p < 0.05).

독립변수 보고

x의 회귀계수는 1.5295로, y에 대하여 유의미한 예측변인인 것으로 나타났다. (t(7) = 5.932, p < 0.05).

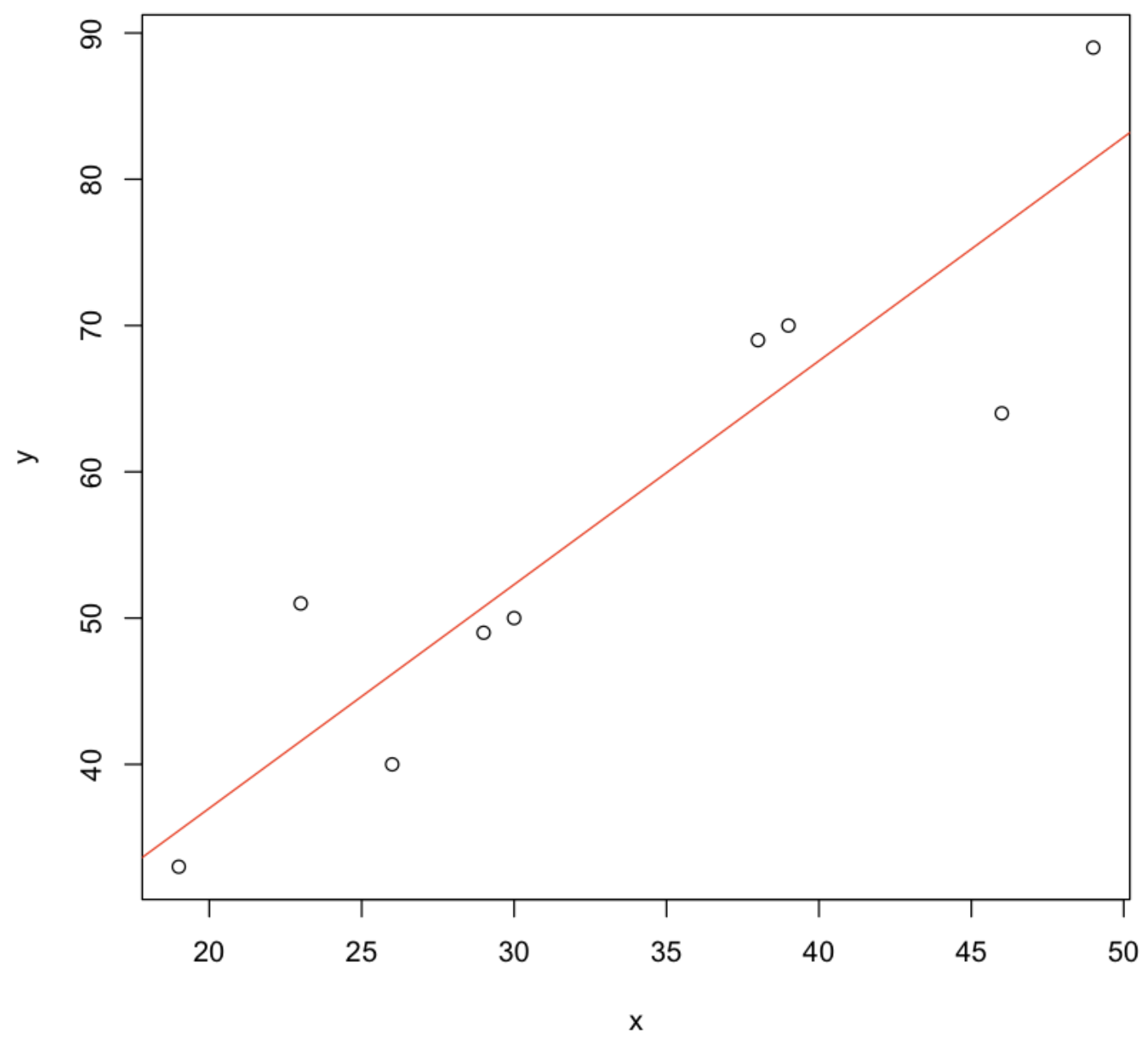
분석결과를 그래프로 표현하기

plot(y~x,data=aircon)
abline(model,col="red")

💻 출력결과