[R] 확률과 확률분포

by 호쌤(이광호) on December 24, 2022

추론통계를 진행하면서 확률과 확률분포가 직접적으로 사용되지는 않지만 많은 통계 과정의 기본 이론이 됩니다. 그러므로 확률과 확률 분포를 이해하는 것은 추론통계의 첫 걸음이라 할 수 있겠습니다.

#01. 확률

• 특정 사건이 일어날 가능성의 척도
• 모든 사건의 확률값은 0과 1사이
• 표본공간 S에 부분집합인 각 사상에 대해 실수값을 가지는 함수의 확률값이 0과 1사이에 있고，전체 확률의 합이 1인 것을 의미
• 표본공간 Q 의 부분집합인 사건 E의 확률은 표본공간의 원소의 개수에 대한 사건 표의 개수의 비율로 확률을 P(E)라고 할 때

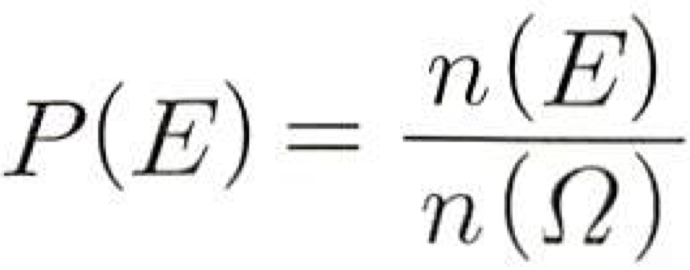
표본공간

• 통계적 실험을 실시할 때 타나날 수 있는 모든 결과들의 집합
• 표본공간에서 임의의 사건 $A$가 일어날 확률 $P(A)$는 항상 0과 1 사이에 있다.

사건

• 표본공간의 부분집합
• 서로 배반인 사건들의 합집합의 확률은 각 사건들의 확률의 합
• 두 사건 A, B가 독립이라면 사건 B의 확률은 A가 일어난다는 가정하에서의 B의 조건부 확률과 동일.

원소

• 나타날 수 있는 개별의 결과들

수학적 확률

$\frac{일어날\,수\,있는\,모든\,경우의\,수}{사건\,A가\,일어나는\,경우의\,수}$

통계적 확률

• 한 사건 $A$가 일어날 확률을 $P(A)$라 할 때 $n$번의 반복시행에서 사건 $A$가 일어날 횟수를 $r$이라고 하면, 상대도수 $\frac{n}{r}$은 $n$이 커점에 따라 확률 $P(A)$에 가까워짐을 알 수 있다. 이러한 $P(A)$를 통계적 확률이라 한다.

조건부 확률

• 사건 $A$가 일어났다는 가정하의 사건 $B$의 확률

• $P(B	A) = \frac{P(A \cap B)}{P(A)}$

#02. 확률변수

• 특정값이 나타날 가능성이 확률적으로 주어지는 변수
• 정의역 (domain)이 표본공간, 치역(range)이 실수값 (0 < y < 1)인 함수

이산형 확률변수

• 이항분포, 기하분포, 다항분포, 베르누이 확률분포, 포아송분포가 있다.
• 0이 아닌 확률값을 갖는 확률 변수를 셀 수 있는 경우 (확률질량함수)

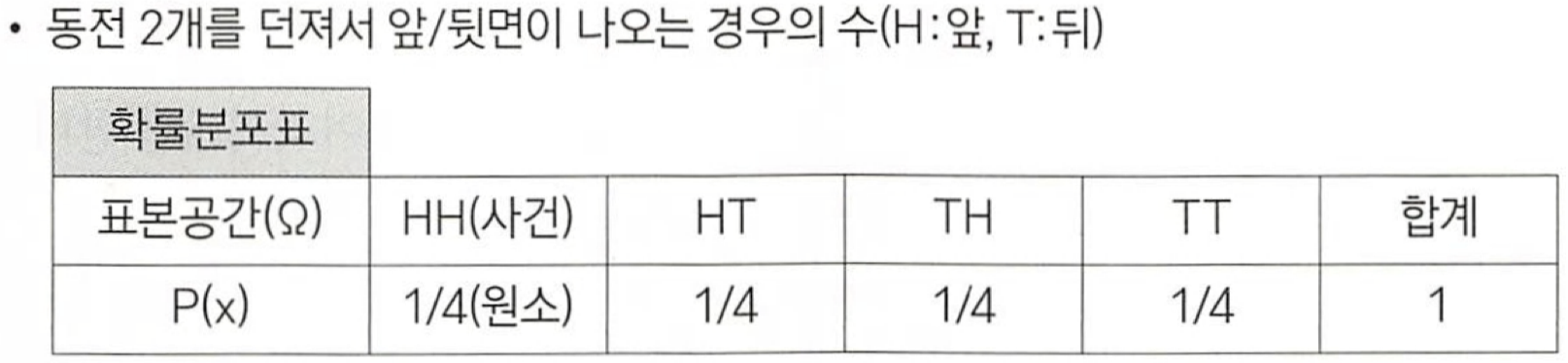
종류	설명
베르누이 확률분포	결과가 2 개만 나오는 경우 (예시 : 동전 던지기, 시험의 합격/불합격 등)
이항분포	베르누이 시행을 n 번 반복했을 때 k 번 성공할 확률
기하분포	성공확률이 p 인 베르누이 시행에서 첫번째 성공이 있기까지 표번 실패할 확률
다항분포	이항분포를 확장한 것으로 세가지 이상의 결과를 가지는 반복 시행에서 발생하는 확률 분포
포아송분포	시간과 공간 내에서 발생하는 사건의 발생횟수에 대한 확률분포 - 책에 오타가 5page 당 10개씩 나온다고 할 때, 한 페이지에 오타가 3개 나올 확률 - 메이저리거인 추신수 선수가 최근 5경기에서 10개의 홈런을 때렸다고 할 때 , 오늘 경기 에서 홈런을 못 칠 확률

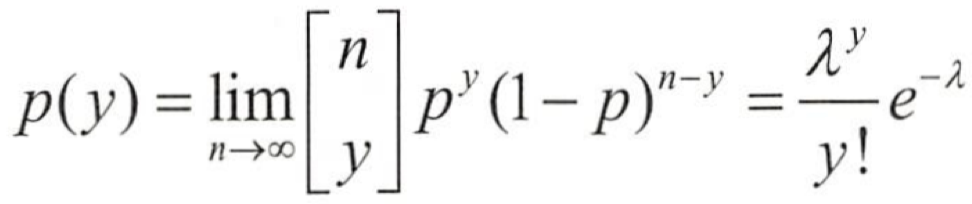
연속형 확률변수

• 균일분포, 정규분포, 지수분포, t-분포가 있다.
• 가능한 값이 실수의 어느 특정구간 전체에 해당하는 확률변수 (확률밀도함수)

• 균일분포
  • 모든 확률변수 X 가 균일한 확률을 가지는 확률분포
  • 다트의 확률분포
• 정규분포

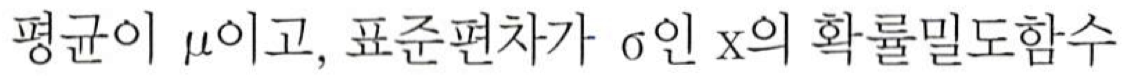
- 표준편차가 클 경우 퍼져보이는 그래프가 나타난다 . - 지수분포
- 어떤 사건이 발생할 때까지 경과 시간에 대한 연속확률분포
- 전자레인지의 수명시간 , 콜센터에 전화가 걸려올 때까지의 시간 , 은행에 고객이 내방 하는데 걸리는 시간 , 정류소에서 버스가 올 때까지의 시간 - t-분포
- 표준정규분포와 같이 평균이 0을 중심으로 좌우가 동일한 분포를 따른다 .
- 표본의 크기가 적을때는 표준 정규분포를 위에서 눌러 높은 것과 같은 형태를 보이지만 표본이 커져서 (30개 이상) 자유도가 증가하면 표준정규분포와 거의 같은 분포가 된다.
- 데이터가 연속형일 경우 활용한다 .
- 두 집단의 평균이 동일한지 알고자 할 때 검정통계량으로 활용